

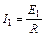 ,F安1
,F安1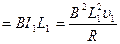 ···································①
···································①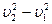 =-2a s1···························································⑤
=-2a s1···························································⑤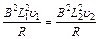 ···························································⑦
···························································⑦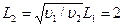 m······················································⑧
m······················································⑧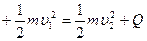 ·······························13·
·······························13·




 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中物理 来源:不详 题型:单选题


查看答案和解析>>
科目:高中物理 来源:不详 题型:填空题

查看答案和解析>>
科目:高中物理 来源:不详 题型:单选题

| A.刚闭合S的瞬间,导体棒中的电流增大 |
| B.刚闭合S的瞬问,导体棒两端电压增大 |
| C.闭含S后,导体棒做减速运动直到停止 |
| D.闭合S后,导体棒做减速运动直到再一次匀速运动 |
查看答案和解析>>
科目:高中物理 来源:不详 题型:实验题

查看答案和解析>>
科目:高中物理 来源:不详 题型:单选题

| A.①③ | B.①④ | C.②③ | D.②④ |
查看答案和解析>>
科目:高中物理 来源:不详 题型:计算题
 的金属杆CD,金属杆与轨道接触良好,整个回路电阻为R,倾斜轨道与水平面夹角为
的金属杆CD,金属杆与轨道接触良好,整个回路电阻为R,倾斜轨道与水平面夹角为 。有一一个与水平轨道平面垂直、方向向下、磁感应强度为B1的匀强磁场;有另一个与倾斜轨道平面垂直、磁感应强度为B2的匀强磁场。为了使CD能够静止,金属杆船在外力F作用下向左匀速运动,试问:
。有一一个与水平轨道平面垂直、方向向下、磁感应强度为B1的匀强磁场;有另一个与倾斜轨道平面垂直、磁感应强度为B2的匀强磁场。为了使CD能够静止,金属杆船在外力F作用下向左匀速运动,试问:
查看答案和解析>>
科目:高中物理 来源:不详 题型:计算题
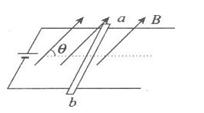
查看答案和解析>>
科目:高中物理 来源:不详 题型:单选题
 ( )
( )| A.维持不动 |
| B.将向使α减小的方向转动 |
C.将向使α增大的方向 转动 转动 |
| D.将向阻碍磁通量增大的方向转动 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com