
 如图所示,矩形盒B的质量为M=5m,底部长度为L,放在水平面上,盒内有一质量为m可视为质点的物体A,A与B、B与地面间的动摩擦因数均为μ,开始时二者均静止,A在B的左端.现瞬间使物体A获得一向右的水平初速度v0,以后物体A与盒B的左右壁碰撞时,B始终向右运动,且每次碰撞时间均极短.当A与B的左壁最后一次碰撞后,B立刻停止运动,A继续向右滑行距离s(s<L)后也停止运动,已知滑动摩擦力等于最大静摩擦力.
如图所示,矩形盒B的质量为M=5m,底部长度为L,放在水平面上,盒内有一质量为m可视为质点的物体A,A与B、B与地面间的动摩擦因数均为μ,开始时二者均静止,A在B的左端.现瞬间使物体A获得一向右的水平初速度v0,以后物体A与盒B的左右壁碰撞时,B始终向右运动,且每次碰撞时间均极短.当A与B的左壁最后一次碰撞后,B立刻停止运动,A继续向右滑行距离s(s<L)后也停止运动,已知滑动摩擦力等于最大静摩擦力.分析 (1)对A应用动能定理可以求出碰撞前A的速度.
(2)A、B发生弹性碰撞,碰撞过程动量守恒,应用动量守恒定律与机械能守恒定律可以求出碰撞后B的速度.
(3)当B停止运动时,A继续向右滑行s(s<L)后停止,根据动能定理列式求出B停止时A的速度;对系统用动量定理可以求出B的运动时间.
解答 解:(1)A第一次与B碰前,B是保持静止状态,
对A,由动能定理得:-μmgL=$\frac{1}{2}$mvA2-$\frac{1}{2}$mv02,
解得:vA=$\sqrt{{v}_{0}^{2}-2μgL}$;
(2)A、B发生弹性碰撞,碰撞过程系统动量守恒、机械能守恒,
以向右为正方向,由动量守恒定律得:mvA=mv1+MvB,
由机械能守恒定律得:$\frac{1}{2}$mvA2=$\frac{1}{2}$mv12+$\frac{1}{2}$MvB2,
解得:vB=$\frac{2}{5}$$\sqrt{{v}_{0}^{2}-2μgL}$,v1=-$\sqrt{{v}_{0}^{2}-2μgL}$;
(3)最后一次碰撞后的过程中,设B停止运动时A的速度为v,
对A由动能定理得:-μmgs=0-$\frac{1}{2}$mv2,解得:v=$\sqrt{2μgs}$,
A、B组成的系统,它在水平方向所受的外力就是地面对盒B的滑动摩擦力,
设盒B运动的总时间为t,选向右为正方向,对系统,由动量定理得:
-μ(m+M)gt=mv-mvA,解得:t=$\frac{\sqrt{{v}_{0}^{2}-2μgL}-\sqrt{2μgs}}{6μg}$;
答:(1)A与B第一次碰撞前,A的速度vA大小为$\sqrt{{v}_{0}^{2}-2μgL}$.
(2)A与B碰撞是弹性正碰,A第一次与B碰后矩形盒B的速度vB大小为$\frac{2}{5}$$\sqrt{{v}_{0}^{2}-2μgL}$.
(3)盒B运动的总时间t为$\frac{\sqrt{{v}_{0}^{2}-2μgL}-\sqrt{2μgs}}{6μg}$.
点评 本题考查动能定理和动量守恒定律、动量定理的综合应用,分析清楚物体运动过程是解题的前提与关键,应用动能定理、动量守恒定律与机械能守恒定律与动量定理可以解题.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:选择题
| A. | 光电效应和康普顿效应揭示了光的粒子性,都表明光子既有能量又有动量 | |
| B. | 一定量气体,在压强不变时,分子每秒对器壁单位面积平均碰撞次数随着温度降低而减少 | |
| C. | 折断的粉笔不能粘合在一起是因为受分子斥力的作用 | |
| D. | 组成原子核的核子的总质量大于该原子核的质量,这个现象是质量亏损 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,竖直放置的两根平行金属导轨之间接有定值电阻R,质量不能忽略的金属棒与两导轨始终保持垂直并良好接触且无摩擦,棒与导轨的电阻均不计,整个装置放在匀强磁场中,磁场方向与导轨平面垂直,棒在竖直向上的恒力F作用下做加速上升运动的一段时间内,以下说法正确的是( )
如图所示,竖直放置的两根平行金属导轨之间接有定值电阻R,质量不能忽略的金属棒与两导轨始终保持垂直并良好接触且无摩擦,棒与导轨的电阻均不计,整个装置放在匀强磁场中,磁场方向与导轨平面垂直,棒在竖直向上的恒力F作用下做加速上升运动的一段时间内,以下说法正确的是( )| A. | 金属棒做得是加速度增加的加速运动 | |
| B. | 力F做的功与安培力做的功的代数和等于棒的机械能增加量 | |
| C. | 金属棒克服安培力做功等于棒产生的电能与回路产生的焦耳热之和 | |
| D. | 力F做的功与重力做的功的代数和等于棒获得的动能和电阻R上放出的热量 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
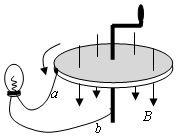 如图是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )
如图是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )| A. | 回路中电流大小恒定 | |
| B. | 回路中电流方向不变,且从b导线流进灯泡,再从a流向旋转的铜盘 | |
| C. | 回路中有大小和方向作周期性变化的电流 | |
| D. | 若将匀强磁场改为仍然垂直穿过铜盘的正弦变化的磁场,不转动铜盘,灯泡中也会有电流流过 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
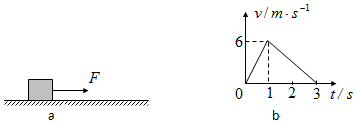
| A. | 物体在3s内的位移s=3m | |
| B. | 恒力F与摩擦力f大小之比F:f=3:1 | |
| C. | 物体与地面的动摩擦因数为μ=0.3 | |
| D. | 3s内恒力做功WF与克服摩擦力做功Wf之比WF:Wf=3:2 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 卫星运行的角速度为$\frac{π}{t}$ | B. | 卫星运行的线速度为π$\frac{R}{t}$ | ||
| C. | 卫星离地面的高度 $\root{3}{\frac{g{R}^{2}{t}^{2}}{{π}^{2}}}$-R | D. | 地球的质量为$\frac{G}{g{R}^{2}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
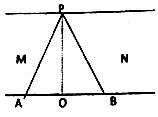 如图所示,MN是流速稳定的河流,水流方向M到N,船在静水中的速度为v,自河一岸的P点开始渡河,第一次船沿PA航行,第二次船沿PB航行,若PA、PB跟河岸垂线PO的夹角相等,两次航行所用的时间分别为TA和TB,则( )
如图所示,MN是流速稳定的河流,水流方向M到N,船在静水中的速度为v,自河一岸的P点开始渡河,第一次船沿PA航行,第二次船沿PB航行,若PA、PB跟河岸垂线PO的夹角相等,两次航行所用的时间分别为TA和TB,则( )| A. | TA>TB | B. | TA<TB | ||
| C. | TA=TB | D. | 无法比较TA和TB的大小 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
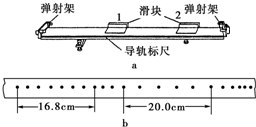 某同学利用打点计时器和气垫导轨做验证动量守恒定律的实验,气垫导轨装置如图(a)所示,它由导轨、滑块、弹射架等组成.在空腔导轨的两个工作面上均匀分布着一定数量的小孔,向导轨空腔内不断通入压缩空气,空气会从小孔中喷出,使滑块稳定地漂浮在导轨上,这样就大大减小了因滑块和导轨之间的摩擦而引起的误差.
某同学利用打点计时器和气垫导轨做验证动量守恒定律的实验,气垫导轨装置如图(a)所示,它由导轨、滑块、弹射架等组成.在空腔导轨的两个工作面上均匀分布着一定数量的小孔,向导轨空腔内不断通入压缩空气,空气会从小孔中喷出,使滑块稳定地漂浮在导轨上,这样就大大减小了因滑块和导轨之间的摩擦而引起的误差.查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com