
 用单摆测定重力加速度的实验如图1所示.
用单摆测定重力加速度的实验如图1所示.| 组次 | 1 | 2 | 3 |
| 摆长L/cm | 80.00 | 90.00 | 100.00 |
| 50 次全振动时间t/s | 90.0 | 95.5 | 100.5 |
| 振动周期T/s | 1.80 | 1.91 | |
| 重力加速度g/(m•s-2) | 9.74 | 9.73 |
分析 ①单摆测定重力加速度的原理是:单摆的周期公式T=2π$\sqrt{\frac{L}{g}}$;在摆角很小的情况下,单摆的振动才是简谐运动;为减小空气阻力的影响,摆球的直径应远小于摆线的长度,选择密度较大的实心金属小球作为摆球.摆长等于摆线的长度加上摆球的半径.
②应用单摆轴公式可以求出重力加速度;
③分析表中实验数据,求出单摆周期、应用单摆周期公式求出重力加速度;
④根据单摆的周期公式变形得出T2与L的关系式,再分析T2-L图象中g与斜率的关系,得到g的表达式.根据重力加速度的表达式,分析各图线与b之间的关系.
解答 解:①为减小实验误差,应选择1m左右的摆线,故选A,为减小空气阻力影响,摆球应选质量大而体积小的金属球,故选D,因此需要的实验器材是AD.
②单摆的周期:T=$\frac{t}{n}$,由单摆周期公式:T=2π$\sqrt{\frac{L}{g}}$可知,重力加速度:g=$\frac{4{π}^{2}L}{{T}^{2}}$=$\frac{4{π}^{2}{n}^{2}L}{{t}^{2}}$.
③由表中实验数据可知,第三组实验中,周期:T=$\frac{100.5s}{50}$=2.01s,代入数据:g=$\frac{4{π}^{2}{n}^{2}L}{{t}^{2}}$解得:g=9.76m/s2;
④根据单摆的周期公式T=2π$\sqrt{\frac{L}{g}}$得,T2=$\frac{4{π}^{2}L}{g}$,根据数学知识可知,T2-L图象的斜率k=$\frac{4{π}^{2}}{g}$,当地的重力加速度g=$\frac{4{π}^{2}}{k}$.
A、若测量摆长时忘了加上摆球的半径,则摆长变成摆线的长度l,则有T2=$\frac{4{π}^{2}L}{g}$,根据数学知识可知,对T2-L图象来说,T2=$\frac{4{π}^{2}L}{g}$+$\frac{4{π}^{2}r}{g}$与b线T2=$\frac{4{π}^{2}L}{g}$斜率相等,两者应该平行,$\frac{4{π}^{2}r}{g}$是截距;故做出的T2-L图象中a线的原因可能是误将悬点到小球上端的距离记为摆长L.故A错误;
B、实验中误将49次全振动记为50次,则周期的测量值偏小,导致重力加速度的测量值偏大,图线的斜率k偏小.故B正确;
C、由图可知,图线c对应的斜率k偏小,根据T2-L图象的斜率k=$\frac{4{π}^{2}}{g}$,当地的重力加速度g=$\frac{4{π}^{2}}{k}$可知,g值大于图线b对应的g值.故C错误.故选:B.
故答案为:①AD;②$\frac{4{π}^{2}{n}^{2}L}{{t}^{2}}$;③2.01;9.76;④B.
点评 简谐运动是一种理想的运动模型,单摆只有在摆角很小,空气阻力影响不计的情况下单摆的振动才可以看成简谐运动,要知道影响实验结论的因素.应用单摆周期公式可以解题;要掌握应用图象法处理实验数据的方法.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中物理 来源: 题型:选择题
| A. | $\frac{{a}_{A}}{{a}_{B}}$=($\frac{R-d}{R+d}$)2 | B. | $\frac{{v}_{A}}{{v}_{B}}$=$\sqrt{\frac{R-d}{R+d}}$ | ||
| C. | $\frac{{ω}_{A}}{{ω}_{B}}$=$\sqrt{\frac{(R-d)^{3}}{(R+d)^{3}}}$ | D. | $\frac{{T}_{A}}{{T}_{B}}$=$\sqrt{\frac{(R+d)^{3}}{{R}^{3}}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
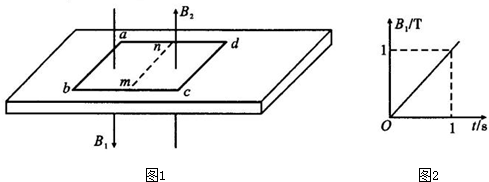
| A. | 导线框中的感应电动势为0.5V | |
| B. | 在t=1s时,导线框所受的安培力大小为1N,方向水平向左 | |
| C. | 导线框中产生俯视逆时针方向的感应电流 | |
| D. | 在0-1s内,导线框一直静止在绝缘长板上 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
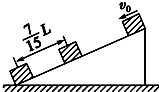 如图所示,小滑块在较长的斜面顶端,以初速度v0=2m/s、加速度a=2m/s2向下滑,在到达底端前1s内,所滑过的距离为斜面长度的$\frac{7}{15}$,求:小滑块在斜面上滑行的时间为多少?
如图所示,小滑块在较长的斜面顶端,以初速度v0=2m/s、加速度a=2m/s2向下滑,在到达底端前1s内,所滑过的距离为斜面长度的$\frac{7}{15}$,求:小滑块在斜面上滑行的时间为多少?查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
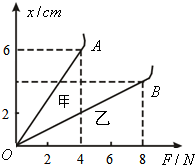 在“探究弹力与弹簧伸长的关系”的实验中.
在“探究弹力与弹簧伸长的关系”的实验中.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com