
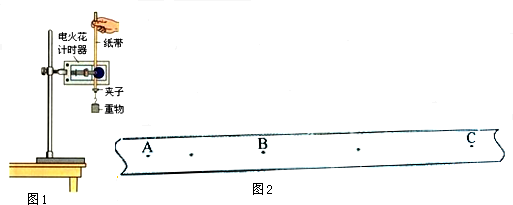
���� �ú��̶ȳ߲���OA�������룬�������������˶��Ĺ�ʽ����������ٶȣ�
��ȷѡȡ��������Ҫ��ȷʵ��ԭ����֪��ʵ��Ŀ�ģ���ȷ��Ҫ��Щ����IJ������Ӷ�ȷ����������ģ��Լ�����Ҫ�����ģ�
���ʵ����������Ҫ���ո�ʵ��ԭ�����˽�ʵ���������������������ݴ����Լ�ע���������ƽ���ٶȴ���˲ʱ�ٶ���B���ٶȣ������������������ļ��ٶȣ�
��� �⣺��1���ú��̶ȳ߲���OA�������룬��ͼ2��ʾ�������ɾ�ֹ��ʼ����ĸ߶�h�������ʱ��t��
�������������˶��Ĺ�ʽ��g=$\frac{2h}{{t}^{2}}$��
��2��A��ʵ������Ҫ����������֮����룬����Ҫ�̶ȳߣ���A��ȷ��
B��ʵ��Ĺ����д���ʱ���Dz���ʱ��ģ��ʲ���Ҫ�������B����
C�����ʱ��ʹ��220V�Ľ�����Դ����D����C��ȷ��
��ѡ��AC��
��3�������ȱ���ֱ���˶������ۣ�g=$\frac{{x}_{BC}-{x}_{AB}}{��2��0.02��^{2}}$=$\frac{0.0917-0.0765}{0.0{4}^{2}}$=9.5m/s2��
ʱ���е��˲ʱ�ٶȵ��ڸù��̵�ƽ���ٶȣ�vB=$\frac{{x}_{AB}+{x}_{BC}}{{t}_{AC}}$=$\frac{0.0765+0.0917}{4��0.02}$=2.1m/s
��4���������Ŀ���ԭ�����������������ܵ�����������Ӱ�죮
�ʴ�Ϊ����1��$\frac{2h}{{t}^{2}}$��
��2��AC��
��3��9.5��2.1��
��4���������������ܵ�����������Ӱ�죮
���� �������Ĺؼ�֪����֤��е���غ㶨�ɵ�ʵ��ԭ���������������ܼ�С���Ͷ��������������ѶȲ������Ի����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
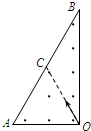 ��ͼ��ʾ��ֱ��������OAB�����ڴ��ڷ���ֱֽ���������ǿ�ų���CΪAB���е㣮���бȺ���ͬ�������ֱ��������������ӣ�������������OC����ͬʱ��O������ų�����BΪ30�� ����˵����ȷ���ǣ�������
��ͼ��ʾ��ֱ��������OAB�����ڴ��ڷ���ֱֽ���������ǿ�ų���CΪAB���е㣮���бȺ���ͬ�������ֱ��������������ӣ�������������OC����ͬʱ��O������ų�����BΪ30�� ����˵����ȷ���ǣ�������| A�� | ����һ�����Ӵ�OA������ų�������һ������һ����OB������ų� | |
| B�� | ����һ�����Ӵ�OB������ų�������һ������һ����CA������ų� | |
| C�� | ���������ӷֱ��A��B��������ų����������ڴų����˶���ʱ��֮��Ϊ2��1 | |
| D�� | ���������ӷֱ��A��B��������ų����������ڴų����˶��Ĺ���뾶֮��Ϊ1��$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ����̫���ܿ����ʵ� | |
| B�� | ƹ�����С�����Կ����ʵ� | |
| C�� | ���������������������ʱ�䣬���ѻ����ʵ� | |
| D�� | �о�����˶�Ա�ļ�������ʱ�������˶�Ա�����ʵ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | Va��Vb��Ta��Tb | B�� | Va��Vb��Ta��Tb | C�� | Va��Vb��Ta��Tb | D�� | Va��Vb��Ta��Tb |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
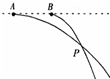 ��ͬһˮƽֱ���ϵ���λ�÷ֱ���ˮƽ���������׳���С��A��B�����˶��켣��ͼ��ʾ�����ƿ���������Ҫʹ�����ڿ���P������������루������
��ͬһˮƽֱ���ϵ���λ�÷ֱ���ˮƽ���������׳���С��A��B�����˶��켣��ͼ��ʾ�����ƿ���������Ҫʹ�����ڿ���P������������루������| A�� | ʹA��B����������� | B�� | A����ٶ�С��B����ٶ� | ||
| C�� | B�����׳� | D�� | ͬʱ�׳����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
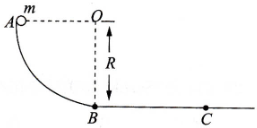 AB����ֱƽ���ڵ��ķ�֮һ�⻬Բ����������¶�B��ˮƽֱ�����У���ͼ��ʾ��һ����Ϊ�ʵ��С����A�����ɾ�ֹ��ʼ�ع���»�����֪Բ����뾶ΪR��С�������Ϊm��С����ˮƽֱ��Ļ���Ħ������Ϊ?������С����C�㴦ͣס�����ƿ�������������
AB����ֱƽ���ڵ��ķ�֮һ�⻬Բ����������¶�B��ˮƽֱ�����У���ͼ��ʾ��һ����Ϊ�ʵ��С����A�����ɾ�ֹ��ʼ�ع���»�����֪Բ����뾶ΪR��С�������Ϊm��С����ˮƽֱ��Ļ���Ħ������Ϊ?������С����C�㴦ͣס�����ƿ��������������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
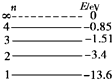 ��ԭ���ܼ���ʾ��ͼ��ͼ��ʾ��������ԭ�Ӵ�n=4���ܼ���n=2���ܼ�ԾǨʱ������ɼ���a����n=3���ܼ���n=2���ܼ�ԾǨʱ������ɼ���b��������
��ԭ���ܼ���ʾ��ͼ��ͼ��ʾ��������ԭ�Ӵ�n=4���ܼ���n=2���ܼ�ԾǨʱ������ɼ���a����n=3���ܼ���n=2���ܼ�ԾǨʱ������ɼ���b��������| A�� | ��ԭ�ӴӸ��ܼ�����ܼ�ԾǨʱ���ܻ����������� | |
| B�� | ��ԭ�Ӵ�n=4���ܼ���n=3���ܼ�ԾǨʱ������������ | |
| C�� | a���ӵ�������b���ӵ������� | |
| D�� | ��ԭ����n=2���ܼ�ʱ����������Ƶ�ʵĹ���������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
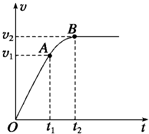 ����Ϊm��������ƽֱ·�����������������̵��ٶ�-ʱ��ͼ����ͼ��ʾ����t1ʱ���������Ĺ��ʱ��ֲ��䣬�����˶���������������������ΪFf��������
����Ϊm��������ƽֱ·�����������������̵��ٶ�-ʱ��ͼ����ͼ��ʾ����t1ʱ���������Ĺ��ʱ��ֲ��䣬�����˶���������������������ΪFf��������| A�� | 0��t1ʱ���ڣ�������ǣ���������Ĵ�С�����������ܵ������� | |
| B�� | t1��t2ʱ���ڣ������Ĺ��ʵ��ڣ�m$\frac{{v}_{1}}{{t}_{1}}$+Ff��v1 | |
| C�� | �����˶�������ٶ�v2=��$\frac{m{v}_{1}}{{F}_{f}{t}_{1}}$+1��v1 | |
| D�� | t1��t2ʱ���ڣ�������ƽ���ٶȵ���$\frac{{v}_{1}+{v}_{2}}{2}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com