练习册

  • 练习册
  • 试题
    精英家教网 > 高中物理 > 题目详情

    如图所示, 半径为r,  质量不计的圆盘盘面与地面相垂直, 圆心处有一个垂直盘面的光滑水平固定轴O,在盘的最右边缘固定一个质量为m的小球A,在O点的正下方离O点的正下方离O点r/2处固定一个质量也为m的小球B. 放开盘让其自由转动, 问 :

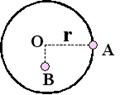    A球转到最低点时的线速度是多少?

    在转动过程中半径OA向左偏离竖直方向的最大角度是多少?                        

    【小题1】

    【小题2】    θ=37°


    解析:

    【小题1】由系统机械能守恒定律 得

    【小题2】设 OA向左偏离竖直方向的最大角度是θ，

    由系统机械能守恒定律 得

    mgr× cosθ – mgr/2× (1+sinθ )=0

    2cosθ=1+sinθ,

    4(1-sin2θ)=1 +2sinθ +sin2θ,

    5sin2θ+2sinθ- 3=0

    Sinθ=0.6  ∴θ=37°

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中物理 来源： 题型：

    如图所示半径为R、r（R＞r）甲、乙两圆形轨道安置在同一竖直平面内，两轨道之间由一条水平轨道（CD）相连，如小球从离地3R的高处A点由静止释放，可以滑过甲轨道，经过CD段又滑上乙轨道后离开两圆形轨道，小球与CD段间的动摩擦因数为μ，其余各段均光滑．
    （1）求小球经过甲圆形轨道的最高点时小球的速度？
    （2）为避免出现小球脱离圆形轨道而发生撞轨现象．试设计CD段的长度．

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    如图所示半径为R的光滑圆形轨道甲，固定在一竖直平面内，它的左右侧分别为光滑的圆弧形轨道AC和光滑斜面轨道DE，斜面DE与水平轨道CD间衔接良好，无能量损失，CD是一条水平轨道，小球与CD段间的动摩擦因数为μ．若小球从离地3R的高处A点由静止自由释放，可以滑过甲轨道，经过CD段又滑上光滑斜面．求：
    （1）小球经过甲圆形轨道的最高点时小球的速度大小；
    （2）为使球到达光滑斜面后返回时，能通过甲轨道，问CD段的长度不超过多少？

    查看答案和解析>>

    科目：高中物理 来源： 题型：

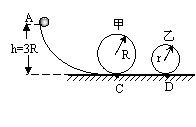     如图所示半径为R、r(R>r)甲、乙两圆形轨道安置在同一竖直平面内，两轨道之间由一条水平轨道(CD)相连，如小球从离地3R的高处A点由静止释放，可以滑过甲轨道，经过CD段又滑上乙轨道后离开两圆形轨道，小球与CD段间的动摩擦因数为μ，其余各段均光滑.为避免出现小球脱离圆形轨道而发生撞轨现象.试设计CD段的长度.

     

     

     

     

     

     

    查看答案和解析>>

    科目：高中物理 来源：2010年大连市长海高中高二下学期期末考试（重点班）物理试题 题型：计算题

    (17分)如图所示,半径为r、圆心为O1的虚线所围的圆形区域内存在垂直纸面向外的匀强磁场,在磁场右侧有一竖直放置的平行金属板M和N,两板间距离为L,在MN板中央各有一个小孔O2、O3,O1、O2、O3在同一水平直线上,与平行金属板相接的是两条竖直放置间距为L的足够长的光滑金属导轨,导体棒PQ与导轨接触良好,与阻值为R的电阻形成闭合回路(导轨与导体棒的电阻不计),该回路处在磁感应强度大小为B,方向垂直纸面向里的匀强磁场中,整个装置处在真空室中,有一束电荷量为+q、质量为m的粒子流(重力不计),以速率v0从圆形磁场边界上的最低点E沿半径方向射入圆形磁场区域,最后从小孔O3射出.现释放导体棒PQ,其下滑h后开始匀速运动,此后粒子恰好不能从O3射出,而从圆形磁场的最高点F射出.求:
    （1）圆形磁场的磁感应强度B′.
    （2）导体棒的质量M.
    （3）棒下落h的整个过程中,电阻上产生的电热.
    （4）粒子从E点到F点所用的时间.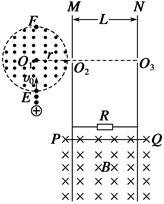

    查看答案和解析>>

    科目：高中物理 来源：2010年大连市高二下学期期末考试（重点班）物理试题 题型：计算题

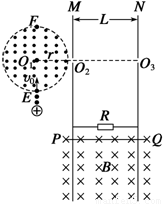
    (17分)如图所示,半径为r、圆心为O1的虚线所围的圆形区域内存在垂直纸面向外的匀强磁场,在磁场右侧有一竖直放置的平行金属板M和N,两板间距离为L,在MN板中央各有一个小孔O2、O3,O1、O2、O3在同一水平直线上,与平行金属板相接的是两条竖直放置间距为L的足够长的光滑金属导轨,导体棒PQ与导轨接触良好,与阻值为R的电阻形成闭合回路(导轨与导体棒的电阻不计),该回路处在磁感应强度大小为B,方向垂直纸面向里的匀强磁场中,整个装置处在真空室中,有一束电荷量为+q、质量为m的粒子流(重力不计),以速率v0从圆形磁场边界上的最低点E沿半径方向射入圆形磁场区域,最后从小孔O3射出.现释放导体棒PQ,其下滑h后开始匀速运动,此后粒子恰好不能从O3射出,而从圆形磁场的最高点F射出.求:

    （1）圆形磁场的磁感应强度B′.

    （2）导体棒的质量M.

    （3）棒下落h的整个过程中,电阻上产生的电热.

    （4）粒子从E点到F点所用的时间.

     

    查看答案和解析>>

    同步练习册答案