
| A. | 太阳的质量约为$\frac{g{R}^{2}}{G}$ | |
| B. | 该行星的质量约为$\frac{10g{R}^{2}}{G}$ | |
| C. | 该行星表面的重力加速度约为$\frac{5}{8}$g | |
| D. | 该行星到太阳的距离约为地球到太阳的距离的7.4×102倍 |
分析 根据万有引力等于重力,结合地球表面的重力加速度和地球的半径可以求出地球的质量,从而得出该行星的质量.根据半径关系和质量关系得出表面重力加速度的感谢,求出行星表面的重力加速度.根据万有引力提供向心力得出周期与轨道半径的关系,结合周期之比求出轨道半径之比.
解答 解:A、地球的半径为R,地球表面的重力加速度为g,根据$G\frac{Mm}{{R}^{2}}=mg$得,地球的质量M=$\frac{g{R}^{2}}{G}$,故A错误.
B、行星质量约为地球的10倍,则行星的质量约为$\frac{10g{R}^{2}}{G}$,故B正确.
C、根据$G\frac{Mm}{{R}^{2}}=mg$得,g=$\frac{GM}{{R}^{2}}$,因为行星质量约为地球的10倍,半径约为地球的4倍,则行星表面的重力加速度约为$\frac{5}{8}$g,故C正确.
D、根据$G\frac{Mm}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}^{2}}$得,r=$\root{3}{\frac{GM{T}^{2}}{4{π}^{2}}}$,因为该行星绕太阳的周期大约是地球绕太阳周期的2万倍,则该行星到太阳的距离约为地球到太阳的距离的7.4×102倍,故D正确.
故选:BCD.
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、万有引力等于重力,2、万有引力提供向心力,并能灵活运用.


科目:高中物理 来源: 题型:选择题
| A. | $\frac{{v}_{0}}{g}$ | B. | $\frac{2{v}_{0}}{g}$ | C. | $\frac{{v}_{0}}{2g}$ | D. | $\frac{\sqrt{2}{v}_{0}}{g}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | △v=0,△Ek=0 | B. | △v=8m/s,△Ek=0 | ||
| C. | △v=8m/s,△Ek=4.8J | D. | △v=0,△Ek=4.8J |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 500J | B. | -500J | C. | -100J | D. | 100J |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 用如图所示装置来验证动量守恒定律,质量为mA的钢球A用细线悬挂于O点,质量为mB的钢球B放在离地面高度为H的小支柱N上,O点到A球球心的距离为L,使悬线伸直并与竖直方向夹角为β,释放后A球摆到最低点时恰与B球对心碰撞,碰撞后,A球把原来静止于竖直方向的轻质指示针OC推到与竖直方向夹角为α处,B球落到地面上,地面上铺有一张盖有复写纸的白纸,保持α角度不变,多次重复上述实验,白纸上记录到多个B球的落点,进而测得B球的水平位移S,当地的重力加速度为g.
用如图所示装置来验证动量守恒定律,质量为mA的钢球A用细线悬挂于O点,质量为mB的钢球B放在离地面高度为H的小支柱N上,O点到A球球心的距离为L,使悬线伸直并与竖直方向夹角为β,释放后A球摆到最低点时恰与B球对心碰撞,碰撞后,A球把原来静止于竖直方向的轻质指示针OC推到与竖直方向夹角为α处,B球落到地面上,地面上铺有一张盖有复写纸的白纸,保持α角度不变,多次重复上述实验,白纸上记录到多个B球的落点,进而测得B球的水平位移S,当地的重力加速度为g.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 0 | B. | $\frac{GM}{(R+h)^{2}}$ | C. | $\frac{GMm}{(R+h)^{2}}$ | D. | $\frac{GM}{{h}^{2}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,一足够大的倾角θ=30°的粗糙斜面上有一个粗细均匀的由同种材料制成的金属线框abcd,线框的质量m=0.6kg,其电阻值R=1.0Ω,ab边长L1=1m,bc边长L2=2m,与斜面之间的动摩擦因数μ=$\frac{{\sqrt{3}}}{9}$.斜面以EF为界,EF上侧有垂直于斜面向上的匀强磁场.一物体通过绝缘细线跨过光滑定滑轮与线框相连,连接线框的细线与斜面平行且线最初处于松弛状态.现先释放线框再释放物体,当cd边离开磁场时线框即以v=2m/s的速度匀速下滑,在ab边运动到EF位置时,细线恰好被拉直绷紧(极短时间内线框速度变化且反向),随即物体和线框一起匀速运动t=2s后开始做匀加速运动.取g=10m/s2,求:
如图所示,一足够大的倾角θ=30°的粗糙斜面上有一个粗细均匀的由同种材料制成的金属线框abcd,线框的质量m=0.6kg,其电阻值R=1.0Ω,ab边长L1=1m,bc边长L2=2m,与斜面之间的动摩擦因数μ=$\frac{{\sqrt{3}}}{9}$.斜面以EF为界,EF上侧有垂直于斜面向上的匀强磁场.一物体通过绝缘细线跨过光滑定滑轮与线框相连,连接线框的细线与斜面平行且线最初处于松弛状态.现先释放线框再释放物体,当cd边离开磁场时线框即以v=2m/s的速度匀速下滑,在ab边运动到EF位置时,细线恰好被拉直绷紧(极短时间内线框速度变化且反向),随即物体和线框一起匀速运动t=2s后开始做匀加速运动.取g=10m/s2,求:查看答案和解析>>
科目:高中物理 来源: 题型:实验题
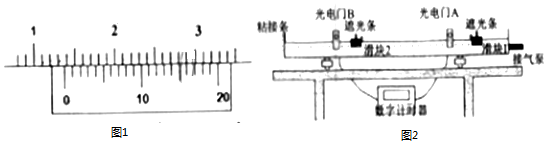
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
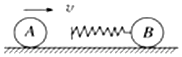 如图所示,在光滑的水平面上放有两个小球A和B其质量mA<mB,B球上固定一轻质弹簧.若将A球以速率v去碰撞静止的B球,碰撞时能量损失不计,下列说法中正确的是( )
如图所示,在光滑的水平面上放有两个小球A和B其质量mA<mB,B球上固定一轻质弹簧.若将A球以速率v去碰撞静止的B球,碰撞时能量损失不计,下列说法中正确的是( )| A. | 当弹簧压缩量最大时,A球速率最小,B球速率最大 | |
| B. | 当弹簧恢复原长时,B球速率最大 | |
| C. | 当A球速率为零时,B球速率最大 | |
| D. | 当B球速率最大时,弹性势能不为零 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com