
 提纯氘核技术对于核能利用具有重大价值.如是从质子、氘核混合物中将质子和氘核分离的原理图,x轴上方有垂直于纸面向外的匀强磁场,初速度为0的质子、氘核混合物经电压为U的电场加速后,从x轴上的A(-L,0)点沿与+x成θ=30°的方向进入第二象限(速度方向与磁场方向垂直),质子刚好从坐标原点离开磁场.已知质子、氘核的电荷量均为+q,质量分别为m、2m,忽略质子、氘核的重力及其相互作用.
提纯氘核技术对于核能利用具有重大价值.如是从质子、氘核混合物中将质子和氘核分离的原理图,x轴上方有垂直于纸面向外的匀强磁场,初速度为0的质子、氘核混合物经电压为U的电场加速后,从x轴上的A(-L,0)点沿与+x成θ=30°的方向进入第二象限(速度方向与磁场方向垂直),质子刚好从坐标原点离开磁场.已知质子、氘核的电荷量均为+q,质量分别为m、2m,忽略质子、氘核的重力及其相互作用.分析 (1)质子在电场中加速,由动能定理可以求出速度.
(2)粒子在磁场中做圆周运动,根据粒子在磁场中运动的周期公式与转过的圆心角可以求出运动时间之比.
(3)由牛顿第二定律求出粒子的轨道半径,然后确定粒子的横坐标.
解答 解:(1)质子在电场中加速,由动能定理得:
qU=$\frac{1}{2}$mv2-0,解得:v=$\sqrt{\frac{2qU}{m}}$;
(2)质子与氘核在磁场中都转过$\frac{1}{6}$个圆周,
做圆周运动的周期:T1=$\frac{2πm}{qB}$,T2=$\frac{2π•2m}{qB}$,
粒子在磁场中的运动时间:t=$\frac{1}{6}$T,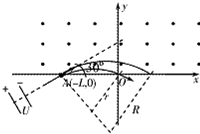
则:t1:t2=T1:T2=1:2;
(3)质子在磁场中运动时,由几何知识得:r=L,
由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,
氘核在电场中加速,由动能定理得:qU=$\frac{1}{2}$•2mv′2-0,
在磁场中,由牛顿第二定律得:qv′B=2m$\frac{v{′}^{2}}{R}$,解得:R=$\sqrt{2}$L,
横坐标:x=R-L=($\sqrt{2}$-1)L;
答:(1)质子进入磁场时速度的大小为$\sqrt{\frac{2qU}{m}}$;
(2)求质子与氘核在磁场中运动的时间之比为1:1;
(3)若在x轴上接收氘核,接收器所在位置的横坐标为($\sqrt{2}$-1)L.
点评 解决本题的关键作出粒子的运动轨迹图,结合几何关系,运用半径公式和周期公式进行求解.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中物理 来源: 题型:选择题

| A. | 物体A做匀加速直线运动,物体B做匀速直线运动 | |
| B. | t2时刻AB两个物体的速度方向相反 | |
| C. | 0-t1时间内A的位移大于B的位移 | |
| D. | t1时刻前A的速度小于B的速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 有一电阻丝阻值在100Ω-200Ω之间,额定功率为0.25W,现用伏安法准确测量它的阻值,实验室除有导线和电键外还备有
有一电阻丝阻值在100Ω-200Ω之间,额定功率为0.25W,现用伏安法准确测量它的阻值,实验室除有导线和电键外还备有查看答案和解析>>
科目:高中物理 来源: 题型:选择题
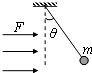 在科学研究中,可以用风力仪直接测量风力的大小,其原理如图所示.仪器中有一根轻质金属丝,悬挂着一个金属球,无风时,金属丝竖直下垂;当有沿水平方向吹来的风时,金属丝偏离竖直方向一个角度,风力越大,偏角越大.那么,风力的大小F和小球质量m、偏角θ的关系是( )
在科学研究中,可以用风力仪直接测量风力的大小,其原理如图所示.仪器中有一根轻质金属丝,悬挂着一个金属球,无风时,金属丝竖直下垂;当有沿水平方向吹来的风时,金属丝偏离竖直方向一个角度,风力越大,偏角越大.那么,风力的大小F和小球质量m、偏角θ的关系是( )| A. | F=mgsinθ | B. | F=$\frac{mg}{cosθ}$ | C. | F=mgtanθ | D. | F=$\frac{mg}{tanθ}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 某段时间内的平均速度等于这段末速度的一半 | |
| B. | 某段时间内的平均速度等于这段中间时刻的瞬时速度 | |
| C. | 在相等时间里速度的变化越来越大 | |
| D. | 在相邻两段相等的时间T内,发生的位移的差为2gT2 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
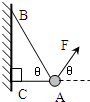 如图所示,物体的质量为2kg,两根轻绳AB和AC的一端连接于竖直墙上,另一端系于物体上,在物体上另施加一个方向与水平线成θ=60°的拉力F,若要使两绳都能伸直,求拉力F的大小范围.
如图所示,物体的质量为2kg,两根轻绳AB和AC的一端连接于竖直墙上,另一端系于物体上,在物体上另施加一个方向与水平线成θ=60°的拉力F,若要使两绳都能伸直,求拉力F的大小范围.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
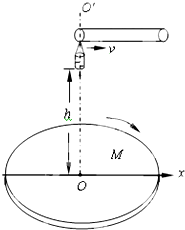 如图所示,M是水平放置的圆盘,绕过其圆心的竖直轴OO'匀速转动,以经过O水平向右的方向作为x轴的正方向.在圆心O正上方距盘面高为h处有一个正在间断滴水的容器,在t=0时刻开始随足够长的传送带沿与x轴平行的方向做匀速直线运动,速度大小为v.已知容器在t=0时滴下第一滴水,以后每当前一滴水刚好落到盘面上时再滴一滴水.问:
如图所示,M是水平放置的圆盘,绕过其圆心的竖直轴OO'匀速转动,以经过O水平向右的方向作为x轴的正方向.在圆心O正上方距盘面高为h处有一个正在间断滴水的容器,在t=0时刻开始随足够长的传送带沿与x轴平行的方向做匀速直线运动,速度大小为v.已知容器在t=0时滴下第一滴水,以后每当前一滴水刚好落到盘面上时再滴一滴水.问:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
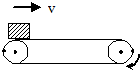 一平直的传送带以速率v=2m/s匀速运行,在传送带最左端把物体轻轻地放到传送带上,经过时间t=6s,物体到达传送带最右端.传送带长L=10m.
一平直的传送带以速率v=2m/s匀速运行,在传送带最左端把物体轻轻地放到传送带上,经过时间t=6s,物体到达传送带最右端.传送带长L=10m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com