
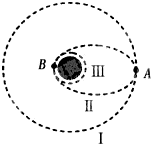
 假设月球半径为R,月球表面的重力加速度为g0,如图所示,飞船首先沿距月球表面高度为3R的圆轨道I运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ(轨道半径可近似当做R)绕月球做圆周运动.下列判断正确的是( )
假设月球半径为R,月球表面的重力加速度为g0,如图所示,飞船首先沿距月球表面高度为3R的圆轨道I运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ(轨道半径可近似当做R)绕月球做圆周运动.下列判断正确的是( )| A. | 飞船在轨道 I上的运行速率为$\sqrt{{g}_{0}R}$ | |
| B. | 飞船在轨道Ⅲ绕月球运动一周所需的时间为2π$\sqrt{\frac{R}{{g}_{0}}}$ | |
| C. | 飞船在Ⅱ轨道A点速率大于在Ⅰ轨道A点速率 | |
| D. | 飞船在Ⅱ轨道B点加速度大于Ⅲ轨道B点加速度 |
分析 在月球表面,万有引力等于重力,在任意轨道,万有引力提供向心力,联立方程即可求解,卫星变轨也就是近心运动或离心运动,根据提供的万有引力和所需的向心力关系确定,飞船在近月轨道Ⅲ绕月球运行,重力提供向心力,根据向心力周期公式即可求解.
解答 解:A、飞船在轨道Ⅰ上,万有引力提供向心力:G$\frac{Mm}{(3R+R)^{2}}=m\frac{{v}^{2}}{3R+R}$,在月球表面,万有引力等于重力得:G$\frac{Mm′}{{R}^{2}}=m{g}_{0}$,解得:v=$\frac{\sqrt{{g}_{0}R}}{2}$,故A错误;
B、设飞船在近月轨道Ⅲ绕月球运行一周所需的时间为T,则:m$\frac{4{π}^{2}}{{T}^{2}}$R=mg0,T=2π$\sqrt{\frac{R}{{g}_{0}}}$,故B正确;
C、飞船在Ⅱ轨道经过A点后开始做近心运动,而在I轨道上做匀速圆周运动,根据近心运动条件提供的向心力大于圆周运动所需向心力可得在II轨道上经过A点时的速率小于在I轨道上经过A点时的速率,故C错误;
D、飞船运动过程中由万有引力产生加速度故在空中同一位置,不管在哪个轨道飞船的加速度相同,故D错误.
故选:B.
点评 本题考查了万有引力定律的应用,知道飞船做圆周运动的向心力由万有引力提供是正确解题的前提,应用万有引力公式与牛顿第二定律可以解题,要掌握应用万有引力定律解题的思路与方法.


科目:高中物理 来源: 题型:多选题
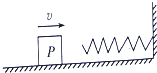 如图所示,物体P以一定的初速度v沿光滑水平面向右运动,与一个右端固定的轻质弹簧相撞,并被弹簧反向弹回,若弹簧在被压缩过程中始终遵守胡克定律,那么在P与弹簧发生相互作用的整个( )
如图所示,物体P以一定的初速度v沿光滑水平面向右运动,与一个右端固定的轻质弹簧相撞,并被弹簧反向弹回,若弹簧在被压缩过程中始终遵守胡克定律,那么在P与弹簧发生相互作用的整个( )| A. | P的加速度大小不断变化,方向也不断变化 | |
| B. | P的加速度大小不断变化,但方向不变 | |
| C. | P和弹簧组成的系统机械能守恒 | |
| D. | P的机械能的改变量小于弹簧对P所做的功 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
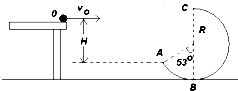 如图所示,将一质量为m=0.1kg的小球自水平平台右端O点以初速度v.水平抛出,小球飞离平台后由A点沿切线落入竖直光滑圆轨道ABC,并沿轨道恰好通过最高点C,圆轨道ABC的形状为半径R=2.5m的圆截去了左上角l27°的圆弧,CB为其竖直直径,(sin53°=0.8 cos53°=0.6,重力加速度g取10m/s2)求:
如图所示,将一质量为m=0.1kg的小球自水平平台右端O点以初速度v.水平抛出,小球飞离平台后由A点沿切线落入竖直光滑圆轨道ABC,并沿轨道恰好通过最高点C,圆轨道ABC的形状为半径R=2.5m的圆截去了左上角l27°的圆弧,CB为其竖直直径,(sin53°=0.8 cos53°=0.6,重力加速度g取10m/s2)求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 当F1>Fsinθ时,一定有两组解 | B. | 当F1<Fsinθ时,一定有两组解 | ||
| C. | 当F1=Fsinθ时,一定有两组解 | D. | 当F1<Fsinθ时,一定无解 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,车间内的天车(有的地区交行车)将一重104N的物体沿着与水平方向成30°角的方向匀速吊起,使物体向斜上方移动了x1=6m,求:
如图所示,车间内的天车(有的地区交行车)将一重104N的物体沿着与水平方向成30°角的方向匀速吊起,使物体向斜上方移动了x1=6m,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题

| 次数 | F(N) | vB2-vA2(m2/s2) | a(m/s2) |
| 1 | 0.60 | 0.77 | 0.80 |
| 2 | 1.04 | 1.61 | 1.68 |
| 3 | 1.42 | 2.34 | |
| 4 | 2.62 | 4.65 | 4.84 |
| 5 | 3.00 | 5.49 | 5.72 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
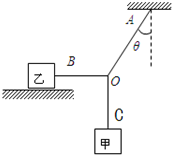 如图所示,质量为m1的物体甲通过三段轻绳悬挂,三段轻绳的结点为O.轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙均处于静止状态.(取g=10m/s2,sin37°=0.6,cos37°=0.8,设最大静摩擦力等于滑动摩擦力)求:
如图所示,质量为m1的物体甲通过三段轻绳悬挂,三段轻绳的结点为O.轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙均处于静止状态.(取g=10m/s2,sin37°=0.6,cos37°=0.8,设最大静摩擦力等于滑动摩擦力)求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | $\frac{T}{2(1-\sqrt{\frac{k}{{n}^{3}}})}$ | B. | $\frac{T}{2(\sqrt{\frac{{n}^{3}}{k}}-1)}$ | C. | $\frac{T}{2(\sqrt{\frac{k}{{n}^{3}}}-1)}$ | D. | $\frac{T}{2(1-\sqrt{\frac{{n}^{3}}{k}})}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com