

分析 (1)对货件进入磁场的过程进行受力分析,根据进入时、离开时的速度相同,分析物件的运动状态,得到加速度的最大值和速度的最小值时刻;然后对该时刻进行受力分析得到加速度的值;对速度最小时刻到货件将出磁场的过程运用动能定理即可得到最小速度;
(2)“次品”一直匀速运动,分析”正品“的运动状态可得到延迟的运动段,再按运动情况进行分段求解即可得延迟时间.
解答 解:(1)线框以速度v0进入磁场,在进入磁场过程中,受安培力F(方向向左)、摩擦力f(方向向右)共同作用而做减速运动;完全进入磁场后,在摩擦力(方向向右)的作用下做加速运动,当ab边到达CC'时速度又恰好等于v0.因此,线框在刚进入磁场时,速度最大,所受安培力F最大,加速度最大,设为am;线框全部进入磁场的瞬间速度最小,设此时线框的速度为v.
线框刚进入磁场时,线框的电动势为?,线框中的电流为i0.
由牛顿第二定律有:F-μmg=mam,
$\left\{\begin{array}{l}F=B{i_0}l\\{i_0}=\frac{ε}{R}\\ ε=Bl{v_0}\end{array}\right.$
解得:${a}_{m}=\frac{F}{m}-μg=\frac{B{i}_{0}l}{m}-ug=\frac{B?l}{mR}-μg$=$\frac{{B}^{2}{l}^{2}{v}_{0}}{mR}-μg$.
在线框完全进入磁场又加速运动到达边界CC'的过程中,线框只受摩擦力,根据动能定理,有:$μmg(d-l)=\frac{1}{2}mv_0^2-\frac{1}{2}m{v^2}$,
解得$v=\sqrt{v_0^2-2μg(d-l)}$.
(2)“次品”(不闭合)在经过磁场的过程中不能产生电流,所以安培力为零,所以,摩擦力也为零,线框进行匀速运动.
由(1)可知,线框ab边到达CC'后将重复线框进入磁场的运动,若线框ab边从AA'到达CC',“次品”(不闭合)比“正品”(闭合)快△T1,则“次品”(不闭合)与“正品”(闭合)因“安检”而延迟时间△T=2△T1.
设“正品”货件进入磁场所用时间为t1,
取此过程中某较短时间间隔△t,在t~(t+△t)的△t内货件速度变化为△v,电流为i,
则由动量定理可得:(μmg-Bil)△t=m△v
即$(μmg-\frac{{B}^{2}{l}^{2}v}{R})△t=m△v$.
对上式在t1时间内进行叠加,可得:$μmg{t}_{1}-\frac{{B}^{2}{l}^{2}}{R}l=mv-m{v}_{0}$
所以,${t}_{1}=\frac{mv-m{v}_{0}+\frac{{B}^{2}{l}^{3}}{R}}{μmg}$=$\frac{{{B^2}{l^3}}}{μmgR}-\frac{{{v_0}-\sqrt{v_0^2-2μg(d-l)}}}{μg}$.
设“正品”货件在磁场中匀加速恢复v0所用时间为t2,
由匀变速速度公式,有:${t_2}=\frac{{{v_0}-v}}{μg}=\frac{{{v_0}-\sqrt{v_0^2-2μg(d-l)}}}{μg}$,
而“次品”货件运动过程不受“安检”的影响,设线框ab边从AA'到达CC'所用时间为T1,由匀速运动规律有:${T}_{1}=\frac{d}{{v}_{0}}$.
可见因“安检”而延迟时间为:△T=2(t1+t2-T1)=$2(\frac{{B}^{2}{l}^{3}}{μmgR}-\frac{d}{{v}_{0}})$.
答:(1)货件在进入磁场的过程中运动加速度的最大值${a_m}=\frac{{{B^2}{l^2}{v_0}}}{mR}-μg$,速度的最小值$v=\sqrt{v_0^2-2μg(d-l)}$;
(2)“次品”(不闭合)与“正品”(闭合)因“安检”而延迟时间$△T=\frac{{2{B^2}{l^3}}}{μmgR}-\frac{2d}{v_0}$.
点评 对时间、发热量、做功这类过程量,我们一定要先分析、了解整个运动过程的基本状态再求解;要注意区分各阶段的情况,进行分段讨论,如我们求位移时,一定要注意各阶段的运动状态是否能统一表示,如要注意是否一直运动等.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中物理 来源: 题型:多选题
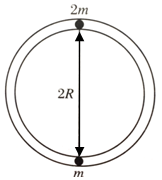 半径为R的光滑细圆环轨道被固定在竖直平面内.内有质量为2m和m的两个小球以相同的角速度经过图示位置.小球直径远小于轨道半径.下列说法正确的是( )
半径为R的光滑细圆环轨道被固定在竖直平面内.内有质量为2m和m的两个小球以相同的角速度经过图示位置.小球直径远小于轨道半径.下列说法正确的是( )| A. | ω<$\sqrt{\frac{g}{R}}$则在图示位置两小球对轨道的作用力方向一定竖直向下 | |
| B. | ω=$\sqrt{\frac{g}{R}}$ 则在图示位置两小球对轨道的作用力为零 | |
| C. | ω>$\sqrt{\frac{g}{R}}$ 则在图示位置两小球对轨道的作用力方向一定竖直向上 | |
| D. | ω=$\sqrt{\frac{3g}{R}}$ 则在图示位置两小球对轨道的作用力为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
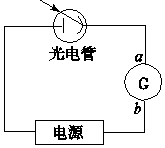
| A. | 增大入射光的强度,光电流增大 | |
| B. | 将入射光换为波长更短的另一种光,光电子的最大初动能变小 | |
| C. | 遏止电压与入射光的频率和强度都有关 | |
| D. | 流过电流表G的电流方向是a流向b(向下) |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
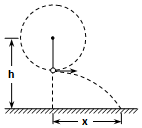 质量m=1kg的小球在长为L=1m的细绳作用下在竖直平面内做圆周运动,细绳能承受的最大拉力Fmax=46N,转轴离地高度h=6m.试求:
质量m=1kg的小球在长为L=1m的细绳作用下在竖直平面内做圆周运动,细绳能承受的最大拉力Fmax=46N,转轴离地高度h=6m.试求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 火箭发射回收是航天技术的一大进步,如图所示,火箭在返回地面前的某段运动,可看成先匀速后减速的直线运动,最后撞落在地面上,不计火箭质量的变化,则( )
火箭发射回收是航天技术的一大进步,如图所示,火箭在返回地面前的某段运动,可看成先匀速后减速的直线运动,最后撞落在地面上,不计火箭质量的变化,则( )| A. | 火箭在匀速下降过程中,机械能守恒 | |
| B. | 火箭在减速下降过程中,携带的检测仪器处于失重状态 | |
| C. | 火箭在减速下降过程中合力做功等于火箭机械能的变化 | |
| D. | 火箭着地时,火箭对地的作用力大于自身的重力 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | “神州十一号”达到与“天宫二号”同一轨道后,从后面加速追上前面的“天宫二号”实现对接 | |
| B. | “伴随卫星”在组合体上空,可以向远离地球的外侧方向喷射气体来实现与组合体以相同的角速度绕地球转动 | |
| C. | “伴随卫星”在组合体上空与组合体以相同的角速度绕地球转动时,加速度小于组合体的加速度 | |
| D. | 航天员景海鹏和陈冬在“天宫二号”中,不受重力作用,处于完全失重状态 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
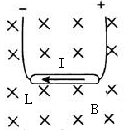 如图所示,长为L=0.2m的导体棒置于磁感应强度B=1.0×10-2T的匀强磁场中,磁场方向垂直于纸面向里,导体棒与磁场方向垂直,若导体棒中的电流I=2.0A,方向水平向左.求:
如图所示,长为L=0.2m的导体棒置于磁感应强度B=1.0×10-2T的匀强磁场中,磁场方向垂直于纸面向里,导体棒与磁场方向垂直,若导体棒中的电流I=2.0A,方向水平向左.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
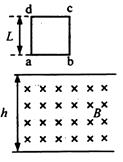 如图所示,边长为L的正方形闭合导体线框abed质量为m,在方向水平的匀强磁场上方某髙度处自由落下并穿过磁场区域.线框在下落过程中形状不变,ab边始终保持与磁场边界线平行,线框平面与磁场方向垂直.已知磁场区域高度h>L,重力加速度为g,下列判断正确的是( )
如图所示,边长为L的正方形闭合导体线框abed质量为m,在方向水平的匀强磁场上方某髙度处自由落下并穿过磁场区域.线框在下落过程中形状不变,ab边始终保持与磁场边界线平行,线框平面与磁场方向垂直.已知磁场区域高度h>L,重力加速度为g,下列判断正确的是( )| A. | 若进入磁场时线框做匀速运动,则离开磁场时线框也一定做匀速运动 | |
| B. | 若进入磁场时线框做减速运动,则离开磁场时线框也一定做减速运动 | |
| C. | 若进入磁场过程中线框产生的热量为mgL,则离开磁场过程中线框产生的热量也一定等于mgL | |
| D. | 若进入磁场过程线框截面中通过的电量为q,则离开磁场过程线框中通过的电量也一定等于q |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,一个内壁光滑的圆锥的轴线垂直于水平面,圆锥固定不动,两个质量相同的球A、B紧贴着内壁,分别在图中所示的水平面内做匀速圆周运动,则( )
如图所示,一个内壁光滑的圆锥的轴线垂直于水平面,圆锥固定不动,两个质量相同的球A、B紧贴着内壁,分别在图中所示的水平面内做匀速圆周运动,则( )| A. | 球A的线速度必大于球B的线速度 | |
| B. | 球A的角速度必大于球B的角速度 | |
| C. | 球A的运动周期必大于球B的运动周期 | |
| D. | 球A的向心加速度必大于球B的向心加速度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com