
| A. | 5:2 | B. | 5:3 | C. | $\sqrt{5}$:2$\sqrt{3}$ | D. | $\sqrt{5}$:$\sqrt{3}$ |
分析 先写出任意两个星星之间的万有引力,求每一颗星星受到的合力,该合力提供它们的向心力.然后用R表达出它们的轨道半径,最后写出用周期和线速度表达的向心力的公式,整理即可的出结果.
解答 解:对第一种的情况,由几何关系知:它们的轨道半径r=$\frac{\sqrt{3}}{3}a$.
任意两个星星之间的万有引力F=$\frac{Gmm}{{a}^{2}}$,
每一颗星星受到的合力,F1=$\sqrt{3}F$
合力提供它们的向心力:$\frac{\sqrt{3}Gmm}{{a}^{2}}=m\frac{4{π}^{2}r}{{T}_{1}^{2}}$
解得T1=$2πa\sqrt{\frac{a}{3Gm}}$;
对第二种情况,相邻的两颗星星之间的万有引力:F=$\frac{Gmm}{{a}^{2}}$
较远的两颗星之间的万有引力:$F′=\frac{Gmm}{(2a)^{2}}$
两侧的星星受到的合力:${F}_{2}=F+F′=\frac{5Gmm}{{4a}^{2}}$
合力提供它们的向心力:$\frac{5Gmm}{4{a}^{2}}=m\frac{4{π}^{2}a}{{T}_{2}^{2}}$
解得T2=$4πa\sqrt{\frac{a}{5Gm}}$
所以:$\frac{{T}_{1}}{{T}_{2}}=\frac{\sqrt{5}}{2\sqrt{3}}$故ABD错误,C正确
故选:C
点评 解决该题首先要理解模型所提供的情景,然后能够列出合力提供向心力的公式,才能正确解答题目.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 某物理兴趣小组用一倾斜固定的气垫导轨做“验证机械能守恒定律”的实验.如图所示,质量为m1的小滑块(含遮光条)放在导轨上的A点,由跨过轻质定滑轮的细绳与质量为m2的钩码相连,导轨上的B点有一光电门,遮光条的宽度为L,A、B两点间的距离为x,气垫导轨的倾角为θ,当地的重力加速度为g,气泵正常工作后,将滑块从A点由静止释放,测得遮光条经过B处光电门的时间为t.
某物理兴趣小组用一倾斜固定的气垫导轨做“验证机械能守恒定律”的实验.如图所示,质量为m1的小滑块(含遮光条)放在导轨上的A点,由跨过轻质定滑轮的细绳与质量为m2的钩码相连,导轨上的B点有一光电门,遮光条的宽度为L,A、B两点间的距离为x,气垫导轨的倾角为θ,当地的重力加速度为g,气泵正常工作后,将滑块从A点由静止释放,测得遮光条经过B处光电门的时间为t.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 三相电源的连接如图所示,电路中的三个交流电压表的示数U 1、U 2、U 3间的关系是( )
三相电源的连接如图所示,电路中的三个交流电压表的示数U 1、U 2、U 3间的关系是( )| A. | U 1:U 2=1:$\sqrt{2}$ | B. | U 1:U 3=1:1 | C. | U 2:U 3=1:1 | D. | U 2:U 3=$\sqrt{3}$:1 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
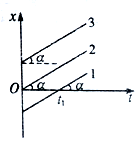
| A. | 三质点都做匀速直线运动 | B. | 只有质点2做匀速直线运动 | ||
| C. | 三质点在t=0位置不同 | D. | 三质点都不做匀速直线运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,质量m=2kg的物体静止于水平地面上的A处,A、B间距L=54m,用大小为F=8N,沿水平方向的恒力拉此物体,经过t0=6s物体运动至B处,取g=10m/s2.
如图所示,质量m=2kg的物体静止于水平地面上的A处,A、B间距L=54m,用大小为F=8N,沿水平方向的恒力拉此物体,经过t0=6s物体运动至B处,取g=10m/s2.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,一木板静止在光滑的水平面上,木板的质量M=4kg,长度L=5m;木板右端放着一小滑块,小滑块的质量m=2kg,其尺寸远小于L.已知小滑块与木板之间的动摩擦因数μ=0.25,现在给木板施加水平向右的拉力F,使小滑块掉下来.取g=10m/s2.
如图所示,一木板静止在光滑的水平面上,木板的质量M=4kg,长度L=5m;木板右端放着一小滑块,小滑块的质量m=2kg,其尺寸远小于L.已知小滑块与木板之间的动摩擦因数μ=0.25,现在给木板施加水平向右的拉力F,使小滑块掉下来.取g=10m/s2.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,质量相等的两物体物体A、B用不可伸长的轻绳连接,在恒力F作用下一起向上做匀加速运动,求此时轻绳对物体B的拉力(g取10m/s2).
如图所示,质量相等的两物体物体A、B用不可伸长的轻绳连接,在恒力F作用下一起向上做匀加速运动,求此时轻绳对物体B的拉力(g取10m/s2).查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示为等量异种电荷周围电场线的分布图,图中M点时两点电荷连线的中点,N点和M点到正电荷的距离相等,若M、N两点电场强度的大小分别为EM和EN,电势分别为φM和φN,则( )
如图所示为等量异种电荷周围电场线的分布图,图中M点时两点电荷连线的中点,N点和M点到正电荷的距离相等,若M、N两点电场强度的大小分别为EM和EN,电势分别为φM和φN,则( )| A. | EM>EN,φM=φN | B. | EM>EN,φM<φN | C. | EM=EN,φM>φN | D. | EM=EN,φM<φN |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com