
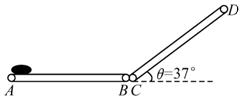
(1)若CD部分不运转,求米袋沿传输带所能上升的最大距离;
(2)若要米袋能被送到D端,CD部分运转速度应满足的条件及米袋从C→D所用时间的取值范围.
解析:(1)由分析可知,米袋在到达B点之前就达到了与传送带相同的速度,由牛顿第二定律,得mgsinθ+μmgcosθ=ma,所以a=g(sinθ+μcosθ)=10 m/s2,所以能滑上的最大距离s=![]() =1.25 m.
=1.25 m.
(2)设CD部分运转速度为v时,米袋恰能到达D点,则:
米袋速度减为v之前加速度a1=g(sinθ+μcosθ)=10 m/s2,米袋速度小于v时加速度a2=g(sinθ-μcosθ)=2 m/s2.由![]() =4.45,解得v=4 m/s.即要把米袋送到D点,CD部分速度vCD≥v=4 m/s,且应沿顺时针方向转动.
=4.45,解得v=4 m/s.即要把米袋送到D点,CD部分速度vCD≥v=4 m/s,且应沿顺时针方向转动.
米袋恰能运到D点(即米袋到达D点时速度恰为零)所用时间最长为tmax=![]() =2.1s.
=2.1s.
若CD部分速度较大,使米袋沿CD上滑时所受摩擦力一直沿皮带向上,则所用时间最短.此种情况米袋加速度一直为a2,由sCD=v0t-![]() a2t2得t=1.16 s,即tmin=1.16 s.所以所求时间范围为1.16 s≤t≤2.1 s.
a2t2得t=1.16 s,即tmin=1.16 s.所以所求时间范围为1.16 s≤t≤2.1 s.


 每课必练系列答案
每课必练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com