
 如图所示,直线MN的下方有竖直向下的匀强电场,场强大小为E=700V/m.在电场区域内有一个平行于MN的挡板PQ;MN的上方有一个半径为R=$\frac{{\sqrt{3}}}{2}$m的圆形弹性围栏,在围栏区域内有图示方向的匀强磁场,磁感应强度大小为B=16.28T.围栏最低点一个小洞b,在b点正下方的电场区域内有一点a,a点到MN的距离d1=45cm,到PQ距离d2=5cm.现将一个质量为m=0.1g,带电量q=2×10-3C的带正电小球(重力不计),从a点由静止释放,在电场力作用下向下运动与挡板PQ相碰后电量减少到碰前的0.8倍,且碰撞前后瞬间小球的动能不变,不计小球运动过程中的空气阻力以及小球与围栏碰撞时的能量损失,试求:(已知1.2510=9.31,1.2511=11.628)
如图所示,直线MN的下方有竖直向下的匀强电场,场强大小为E=700V/m.在电场区域内有一个平行于MN的挡板PQ;MN的上方有一个半径为R=$\frac{{\sqrt{3}}}{2}$m的圆形弹性围栏,在围栏区域内有图示方向的匀强磁场,磁感应强度大小为B=16.28T.围栏最低点一个小洞b,在b点正下方的电场区域内有一点a,a点到MN的距离d1=45cm,到PQ距离d2=5cm.现将一个质量为m=0.1g,带电量q=2×10-3C的带正电小球(重力不计),从a点由静止释放,在电场力作用下向下运动与挡板PQ相碰后电量减少到碰前的0.8倍,且碰撞前后瞬间小球的动能不变,不计小球运动过程中的空气阻力以及小球与围栏碰撞时的能量损失,试求:(已知1.2510=9.31,1.2511=11.628)分析 (1)、在与挡板PQ相碰碰撞时没有能量损失,只有电量损失.所以每碰一次,回弹的高度都会增加.向下运动时,电场力做正功,向上运动时,电场力做负功.由能量关系可求出第一次碰撞后小球向上运动的高度.
(2)、通过第一问的解题方法,表示出碰撞n次时,小球上升的高度xn,如果满足xn>d1+d2,小球即可进入圆形磁场区域,由动能定理即可求出此时进入磁场区域的速度.
(3)、因第二问已求出进入磁场的速度,小球在磁场中做圆周运动,即可求出小球的轨道半径和周期,通过几何关系求出小球的偏转角,从而判断碰撞的次数.
解答 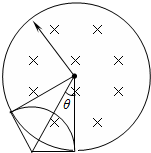 解:(1)设小球第一次与挡板相碰后向上运动距离为x1,则
解:(1)设小球第一次与挡板相碰后向上运动距离为x1,则
qEd2=0.8qEx1
x1=1.25d2=6.25(cm)
(2)设第n次与挡板PQ相碰后向上运动距离为xn,则:0.8nqExn=qEd2
要使小球能进入围栏,应有:
xn>d1+d2
综上:1.25n>10
所以:当小球与挡板碰撞11次后,小球将第一次进入围栏内
设进入速度大小为v,则应有:$qE{d_2}-{0.8^{11}}qE({d_1}+{d_2})=\frac{1}{2}m{v^2}$
解得:v=14(m/s)
(3)小球进入圆形围栏后,在洛伦兹力作用下做匀速圆周运动,如图所示$q'vB=m\frac{v^2}{r}$
所以轨道半径 $r=\frac{mv}{q'B}=0.5$(m)
运动周期 $T=\frac{2πr}{v}=\frac{π}{14}$(s)
图中 $tanθ=\frac{r}{R}=\frac{0.5}{0.866}$所以 θ=30°
即,当小球每转过120°圆周就与围栏碰撞一次,最终经过5次碰撞,从小洞b离开围栏区,
故在围栏内运动时间为:$t=6×\frac{1}{3}T=\frac{π}{7}$(s)=0.45s
答:(1)求出小球第一次与挡板PQ相碰后向上运动的距离为6.25cm.
(2)小球第一次从小洞b进入围栏时的速度大小为14m/s.
(3)小球从第一次进入围栏到离开围栏经历的时间$\frac{π}{7}$.
点评 解决此种类型的题,对于过程的分析成了解决问题的关键,在各个过程中要分析清楚变化的量和不变的量.根据对过程的分析,画出草图,充分利用相关的几何知识来解决问题.该题还考察了边界问题,要注意分析磁场边界对运动轨迹的影响.


科目:高中物理 来源: 题型:选择题
| A. | 5:3:1 | B. | 1:3:5 | C. | 9:4:1 | D. | 1:4:9 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | 物体在第4 s末改变运动方向 | |
| B. | 0-4 s内的加速度大于6-8 s内的加速度 | |
| C. | 第8 s末物体离出发点最远 | |
| D. | 前6 s内的位移为12m |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 某学校课外兴趣小组,在一次科学探究活动中,用多用电表对未知电阻进行测量,先把选择开关旋到电阻挡的“×1k“挡,然后进行欧姆调零后,再将红、黑表笔搭在未知电阻两端,此时指针位置如图所示,那么测得该电阻的阻值是1.4×104Ω.
某学校课外兴趣小组,在一次科学探究活动中,用多用电表对未知电阻进行测量,先把选择开关旋到电阻挡的“×1k“挡,然后进行欧姆调零后,再将红、黑表笔搭在未知电阻两端,此时指针位置如图所示,那么测得该电阻的阻值是1.4×104Ω.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 在汽车无极变速器中,存在如图所示的装置,A是与B同轴相连的齿轮,C是与D同轴相连的齿轮,A、C、M为相互咬合的齿轮.已知齿轮A、C规格相同,半径为R,齿轮B、D规格也相同,半径为1.5R,齿轮M的半径为0.9R.当齿轮M如图方向转动时以下说法错误的是( )
在汽车无极变速器中,存在如图所示的装置,A是与B同轴相连的齿轮,C是与D同轴相连的齿轮,A、C、M为相互咬合的齿轮.已知齿轮A、C规格相同,半径为R,齿轮B、D规格也相同,半径为1.5R,齿轮M的半径为0.9R.当齿轮M如图方向转动时以下说法错误的是( )| A. | 齿轮D和齿轮B的转动方向相同 | |
| B. | 齿轮D和齿轮A的转动周期之比为1:1 | |
| C. | 齿轮M和齿轮B边缘某点的线速度大小之比为2:3 | |
| D. | 齿轮M和齿轮C的角速度大小之比为9:10 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 国庆节时,五颜六色的氢气球将节日装扮得靓丽多姿.如图所示,一氢气球通过软绳与地面上的石块相连,石块质量为m,由于风的作用,使软绳偏离竖直方向,当氢气球和石块相对地面静止时,与石块相连的绳端切线与水平方向成θ角,不计风对石块的作用,则下列说法中正确的是( )
国庆节时,五颜六色的氢气球将节日装扮得靓丽多姿.如图所示,一氢气球通过软绳与地面上的石块相连,石块质量为m,由于风的作用,使软绳偏离竖直方向,当氢气球和石块相对地面静止时,与石块相连的绳端切线与水平方向成θ角,不计风对石块的作用,则下列说法中正确的是( )| A. | 绳子的拉力为$\frac{mg}{sinθ}$ | |
| B. | 绳子的拉力一定小于mg,否则石块将会被风吹动的氢气球带离地面 | |
| C. | 石块受到地面作用力不等于绳子拉力的水平分力 | |
| D. | 石块受到地面作用力和绳子拉力的合力大于石块的重力 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,在O点放一个正电荷,在过O点的竖直平面内的A点,自由释放一个带正电的小球,小球的质量为m、电荷量为q.小球落下的轨迹如图中虚线所示,它与以O为圆心、R为半径的圆(图中实线表示)相交于B、C两点,O、C在同一水平线上,∠BOC=30°,A距离OC的竖直高度为h.若小球通过B点的速度为v,试求:
如图所示,在O点放一个正电荷,在过O点的竖直平面内的A点,自由释放一个带正电的小球,小球的质量为m、电荷量为q.小球落下的轨迹如图中虚线所示,它与以O为圆心、R为半径的圆(图中实线表示)相交于B、C两点,O、C在同一水平线上,∠BOC=30°,A距离OC的竖直高度为h.若小球通过B点的速度为v,试求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 如果质点振动的位移与时间的关系遵从正弦函数的规律,这样的振动叫做简谐振动 | |
| B. | 如果质点做简谐振动,则质点振动的动能和弹性势能的总和保持不变 | |
| C. | 回复力F=-kx,是简谐振动的条件,回复力F只能是弹力 | |
| D. | 弹簧振子的振动在考虑空气阻力时,做的也是简谐振动 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com