
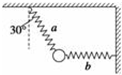
 如图所示,两轻质弹簧a、b悬挂一质量为m的小铁球,小铁球处于平衡状态,a弹簧与竖直方向成30°角,b弹簧水平,a、b两弹簧的劲度系数分别为k1、k2,重力加速度为g,则下列说法正确的是( )
如图所示,两轻质弹簧a、b悬挂一质量为m的小铁球,小铁球处于平衡状态,a弹簧与竖直方向成30°角,b弹簧水平,a、b两弹簧的劲度系数分别为k1、k2,重力加速度为g,则下列说法正确的是( )| A. | a弹簧的伸长量为$\frac{\sqrt{3}mg}{3{k}_{1}}$ | |
| B. | a、b两弹簧的伸长量的比值为$\frac{2{k}_{2}}{{k}_{1}}$ | |
| C. | 若弹簧b的左端松脱,则松脱瞬间小铁球的加速度为$\frac{g}{2}$ | |
| D. | 若弹簧a的下端松脱,则松脱瞬间小铁球的加速度为$\sqrt{3}$g |
分析 对小球受力分析,受到重力和两个弹簧的弹力,根据平衡条件并运用合成法得到两个弹力之比,再结合胡克定律求解出伸长量之比,根据小球平衡由弹簧松脱得出弹力变化情况,再据牛顿第二定律分析加速度情况.
解答 解:A、由受力图知,弹簧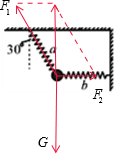 a中弹力${F}_{1}=\frac{mg}{cosα}=\frac{mg}{\frac{\sqrt{3}}{2}}=\frac{2\sqrt{3}mg}{3}$,据胡克定律a弹簧的伸长量为$\frac{2\sqrt{3}mg}{3{k}_{1}}$,故A错误;
a中弹力${F}_{1}=\frac{mg}{cosα}=\frac{mg}{\frac{\sqrt{3}}{2}}=\frac{2\sqrt{3}mg}{3}$,据胡克定律a弹簧的伸长量为$\frac{2\sqrt{3}mg}{3{k}_{1}}$,故A错误;
B、对小球受力分析,受到重力和两个弹簧的弹力,如图
根据平衡条件,有:$\frac{{F}_{2}}{{F}_{1}}=sin30°$=$\frac{1}{2}$
根据胡克定律,有:
F1=k1x1
F2=k2x2
解得:$\frac{{x}_{1}}{{x}_{2}}=\frac{2{k}_{2}}{{k}_{1}}$,故B正确;
C、由受力图可知,弹簧b中弹力${F}_{2}={F}_{1}sinα=\frac{2\sqrt{3}mg}{3}•\frac{1}{2}=\frac{\sqrt{3}mg}{3}$,若弹簧b的左端松脱,则松脱瞬间a弹簧的弹力不变,故小球所受重力和a弹簧弹力的合力与F2大小相等方向相反,故小球的加速度a=$\frac{{F}_{2}}{m}=\frac{\sqrt{3}}{3}g$,故C错误;
D、由受力图知,弹簧a中弹力${F}_{1}=\frac{mg}{cosα}=\frac{mg}{\frac{\sqrt{3}}{2}}=\frac{2\sqrt{3}mg}{3}$,若弹簧a的左端松脱,则松脱瞬间b弹簧的弹力不变,故小球所受重力和b弹簧弹力的合力与F1大小相等方向相反,故小球的加速度a=$\frac{{F}_{1}}{m}=\frac{2\sqrt{3}}{3}g$,故D错误.
故选:B.
点评 本题考查共点力平衡条件的运用,关键是作图,三力中两个力的合力一定与第三个力等值、反向、共线,知道一个弹簧弹力变化的瞬间,另一弹簧弹力保持不变.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 某待测电阻的阻值大约在20kΩ~50kΩ之间,现要测量其电阻,实验室提供下列可选用的器材:
某待测电阻的阻值大约在20kΩ~50kΩ之间,现要测量其电阻,实验室提供下列可选用的器材:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 物体所受合力的方向就是物体的运动方向 | |
| B. | 物体受到的合力为零时,它一定处于静止状态 | |
| C. | 物体受到不为零的合力作用时,它的运动状态要发生改变 | |
| D. | 物体做匀速圆周运动时,它的运动状态不发生改变 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
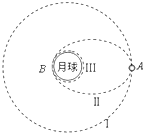 “神州七号”飞船的成功飞行为我国在2010年实现探月计划-“嫦娥工程”获得了宝贵的经验.假设月球半径为R,月球表面的重力加速度为g0,飞船在距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.则( )
“神州七号”飞船的成功飞行为我国在2010年实现探月计划-“嫦娥工程”获得了宝贵的经验.假设月球半径为R,月球表面的重力加速度为g0,飞船在距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.则( )| A. | 飞船在轨道Ⅰ上的运行速率v=$\frac{1}{2}$$\sqrt{{g}_{0}R}$ | |
| B. | 飞船在A点处点火时,动能增加 | |
| C. | 飞船在轨道Ⅰ上运行速率大于在轨道Ⅲ上的运行速率 | |
| D. | 飞船在轨道Ⅲ绕月球运行一周所需的时间为T=2π$\sqrt{\frac{R}{{g}_{0}}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
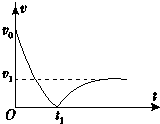 从地面上以初速度v0竖直上抛一个小球.若小球在运动过程中所受空气阻力与速率成正比,小球运动的速率随时间变化的规律如图所示,t1时刻到达最高点,落地速率为v1,且落地前小球已经做匀速运动,则小球上升过程的平均速度<$\frac{{v}_{0}}{2}$(选填“>”、“=”或“<”),小球抛出瞬间的加速度大小为(1+$\frac{{v}_{0}}{{v}_{1}}$)g.
从地面上以初速度v0竖直上抛一个小球.若小球在运动过程中所受空气阻力与速率成正比,小球运动的速率随时间变化的规律如图所示,t1时刻到达最高点,落地速率为v1,且落地前小球已经做匀速运动,则小球上升过程的平均速度<$\frac{{v}_{0}}{2}$(选填“>”、“=”或“<”),小球抛出瞬间的加速度大小为(1+$\frac{{v}_{0}}{{v}_{1}}$)g.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
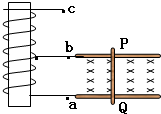 如图,铁芯上绕有线圈,a、c是线圈的两端,b是中心抽头,将a、b分别接在一对平行金属导轨上,在金属导轨上有一与其接触良好的金属棒PQ.导轨处在匀强磁场中,若a、c两点的电势都高于b点的电势,则PQ的运动应是( )
如图,铁芯上绕有线圈,a、c是线圈的两端,b是中心抽头,将a、b分别接在一对平行金属导轨上,在金属导轨上有一与其接触良好的金属棒PQ.导轨处在匀强磁场中,若a、c两点的电势都高于b点的电势,则PQ的运动应是( )| A. | 向右加速 | B. | 向右减速 | C. | 向左加速 | D. | 向左减速 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com