
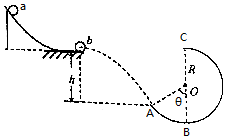
 如图所示,一弧形轨道与光滑水平轨道平滑连接,水平轨道的末端静止着一质量为2m的小球b.从弧形轨道的某处由静止释放另一质量为m的小球a,a球沿轨道下滑后与b球发生弹性正碰,碰后b球以某一速度水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失).已知光滑平台离A的竖直高度为h,圆弧的半径为R,OA与竖直方向的夹角为θ,小球均可视为质点(重力加速度为g),求:
如图所示,一弧形轨道与光滑水平轨道平滑连接,水平轨道的末端静止着一质量为2m的小球b.从弧形轨道的某处由静止释放另一质量为m的小球a,a球沿轨道下滑后与b球发生弹性正碰,碰后b球以某一速度水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失).已知光滑平台离A的竖直高度为h,圆弧的半径为R,OA与竖直方向的夹角为θ,小球均可视为质点(重力加速度为g),求:分析 (1)利用运动的合成和分解,结合速度偏向角公式,即可求出小球b在A点的速度;
(2)利用b球到达A点时的速度vA结合动量守恒和动能守恒,即可求出a球与b球碰撞前、后的瞬时速度;
(3)从A到C对小球b运用动能定理,对C点小球进行受力分析,再结合牛顿第二定律,即可求出小球b通过圆弧的最高点C时,对轨道的压力.
解答 解:(1)设b球平抛的初速度为v0,根据平抛运动速度规律可得:
vx=v0①
vy=gt ②
h=$\frac{1}{2}g{t}^{2}$③
速度偏向角公式有:tanθ=$\frac{{v}_{y}}{{v}_{x}}$=$\frac{gt}{{v}_{0}}$④
联立①②③④可得:vx=$\frac{\sqrt{2gh}}{tanθ}$ ⑤,vy=$\sqrt{2gh}$⑥
b球到达A点时的速度:vA=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$⑦
联立⑤⑥⑦式可得:vA=$\sqrt{2gh(\frac{1}{ta{n}^{2}θ}+1)}$⑧
(2)ab两球碰撞,根据动量守恒定律可得:mv1=2mv0+mv2⑨
根据能量守恒可得:$\frac{1}{2}m{v}_{1}^{2}$=$\frac{1}{2}•2m{v}_{0}^{2}$+$\frac{1}{2}{mv}_{2}^{2}$⑩
联立⑨⑩式可得,a球与b球碰撞前速度:v1=$\frac{3\sqrt{2gh}}{2tanθ}$
a球与b球碰撞后速度:v2=$-\frac{\sqrt{2gh}}{2tanθ}$
(3)对b球从A到C点的过程运用动能定理可得:-2mgR(1+cosθ)=$\frac{1}{2}•2m{v}_{C}^{2}$-$\frac{1}{2}•2m{v}_{A}^{2}$⑪
C点对b球运用牛顿第二定律可得:N+2mg=2m•$\frac{{v}_{C}^{2}}{R}$⑫
根据牛顿第三定律可得,C时小球b对轨道的压力:N′=N⑬
联立⑪⑫⑬式可得:N′=mg($\frac{4h}{Rta{n}^{2}θ}$+$\frac{4h}{R}$-4cosθ-6)
答:(1)b球到达A点时的速度vA为$\sqrt{2gh(\frac{1}{ta{n}^{2}θ}+1)}$;
(2)a球与b球碰撞前的瞬时速度大小为$\frac{3\sqrt{2gh}}{2tanθ}$,方向水平向右,a球与b球碰撞前的瞬时速度大小为$\frac{3\sqrt{2gh}}{2tanθ}$,方向水平向左;
(3)若b球能够通过圆弧的最高点,则到达圆弧最高点C时,对轨道的压力为mg($\frac{4h}{Rta{n}^{2}θ}$+$\frac{4h}{R}$-4cosθ-6).
点评 本题考查动能定理动量守恒定律的综合运用,解题关键是要分好过程,对研究对象进行受力分析,选择合适的规律解题;要求大家牢记平抛运动的规律,以及弹性碰撞过程所满足的动量守恒和动能守恒.


科目:高中物理 来源: 题型:多选题
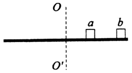 如图所示,水平圆盘上有两个材料相同的小木块a和b(可视为质点),其质量分别为2m和m,与转轴OO′的距离分别为l和2l.若圆盘从静止开始绕转轴缓慢地加速转动,下列说法正确的是( )
如图所示,水平圆盘上有两个材料相同的小木块a和b(可视为质点),其质量分别为2m和m,与转轴OO′的距离分别为l和2l.若圆盘从静止开始绕转轴缓慢地加速转动,下列说法正确的是( )| A. | 一定是b先开始滑动 | |
| B. | 在a和b发生滑动前向心力之比1:1 | |
| C. | 在a和b发生滑动前向心加速度之比1:1 | |
| D. | 在a和b发生滑动前线速度之比为1:2 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,A、B是电场中的两点,设一试探电荷先后置于A、B两处时所受电场力分别为FA和FB,则FA和FB的大小关系是( )
如图所示,A、B是电场中的两点,设一试探电荷先后置于A、B两处时所受电场力分别为FA和FB,则FA和FB的大小关系是( )| A. | FA=FB | B. | FA<FB | ||
| C. | FA>FB | D. | 试探电荷正负不明,无法判断 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 放在粗糙水平地面上的滑块,受到随时间t变化的水平拉力F(如图甲所示)作用,其运动的图象如图乙所示,重力加速度g=10m/s2,则下列说法正确的是( )
放在粗糙水平地面上的滑块,受到随时间t变化的水平拉力F(如图甲所示)作用,其运动的图象如图乙所示,重力加速度g=10m/s2,则下列说法正确的是( )| A. | 第1s末滑块所受摩擦力的f的大小为4N | |
| B. | 滑块与水平面间的动摩擦因数μ=0.4 | |
| C. | 1~4s内,力F对滑块做功为48J | |
| D. | 1~4s内,摩擦力对滑块做功为-16J |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
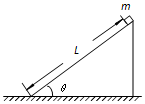 如图所示,倾角为θ=37°的光滑斜面固定在地面上,斜面的长度为L=3.0m;质量m=0.10kg的滑块(可视为质点)从斜面顶端由静止滑下;已知sin37°=0.60,cos37°=0.80,空气阻力可忽略不计,重力加速度g取10m/s2.求:
如图所示,倾角为θ=37°的光滑斜面固定在地面上,斜面的长度为L=3.0m;质量m=0.10kg的滑块(可视为质点)从斜面顶端由静止滑下;已知sin37°=0.60,cos37°=0.80,空气阻力可忽略不计,重力加速度g取10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
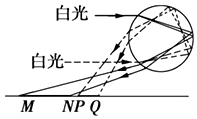 虹和霓是太阳光在水珠内分别经过一次和两次反射后出射形成的,可用白光照射玻璃球来说明.两束平行白光照射到透明玻璃球后,在水平的白色桌面上会形成MN和PQ两条彩色光带,光路如图8所示.关于照到M、N、P、Q点的单色光的说法中正确的是( )
虹和霓是太阳光在水珠内分别经过一次和两次反射后出射形成的,可用白光照射玻璃球来说明.两束平行白光照射到透明玻璃球后,在水平的白色桌面上会形成MN和PQ两条彩色光带,光路如图8所示.关于照到M、N、P、Q点的单色光的说法中正确的是( )| A. | M、N、P、Q点的光的颜色分别为紫、红、红、紫 | |
| B. | M点的光的波动性较N点的光更显著 | |
| C. | 在同一单缝衍射装置上做实验,用P点的光得到的衍射图样的中央明纹宽度较Q点的光更窄 | |
| D. | 水中相同深度处有两个光源,其颜色分别与P、Q两点的光同色,在其正上方的水面之上,同等条件下观测,同P色的点光源在水下的像最深,且其照亮水面的面积最大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,静止在水平面上、质量为3kg的物体,在水平拉力F作用下从A点运动到B点的过程中,F对物体做功10J,摩擦力对物体做功-4J,则物体在B点时速度的大小为( )
如图所示,静止在水平面上、质量为3kg的物体,在水平拉力F作用下从A点运动到B点的过程中,F对物体做功10J,摩擦力对物体做功-4J,则物体在B点时速度的大小为( )| A. | 2 m/s | B. | 4 m/s | C. | 6 m/s | D. | 10 m/s |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com