
 如图所示,是某同学站在压力传感器上,做下蹲-起立的动作时记录的力随时间变化的图线,纵坐标为力(单位为牛顿,横轴的单位为时间.由图可知( )
如图所示,是某同学站在压力传感器上,做下蹲-起立的动作时记录的力随时间变化的图线,纵坐标为力(单位为牛顿,横轴的单位为时间.由图可知( )| A. | 该同学做了两次下蹲-起立的动作 | |
| B. | 该同学做了一次下蹲-起立的动作 | |
| C. | 下蹲过程中人处于失重状态 | |
| D. | 下蹲过程中先处于超重状态后处于失重状态 |
分析 失重状态:当物体对接触面的压力小于物体的真实重力时,就说物体处于失重状态,此时有向下的加速度;超重状态:当物体对接触面的压力大于物体的真实重力时,就说物体处于超重状态,此时有向上的加速度.人下蹲过程分别有失重和超重两个过程,先是加速下降失重,到达一个最大速度后再减速下降超重,起立也是如此.
解答 解:人下蹲动作分别有失重和超重两个过程,先是加速下降失重,到达一个最大速度后再减速下降超重对应先失重再超重,起立对应先超重再失重,对应图象可知,该同学做了一次下蹲-起立的动作,A错误;
由图象看出两次超重的时间间隔就是人蹲在地上持续的时间,约2s,B正确;
下蹲过程既有失重又有超重,且先失重后超重,C、D均错误;
故选:B
点评 本题考察物理知识与生活的联系,注意细致分析物理过程,仔细观察速度的变化情况,与超失重的概念联系起来加以识别


科目:高中物理 来源: 题型:多选题
| A. | 匀速圆周运动的速度大小保持不变,所以做匀速圆周运动的物体没有加速度 | |
| B. | 做匀速圆周运动的物体,虽然速度大小不变,但方向时刻都在改变,所以必有加速度 | |
| C. | 做匀速圆周运动的物体,加速度的大小保持不变,所以是匀变速曲线运动 | |
| D. | 匀速圆周运动加速度的方向时刻都在改变,所以匀速圆周运动一定是变加速曲线运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 静止的物体一定没有受到力的作用 | |
| B. | 运动的物体不受力就会停止下来 | |
| C. | 正在运动的物体一定受到力的作用 | |
| D. | 运动的物体,如果不受力的作用,将永远运动下去 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,三个同心圆是同一个点电荷周围的三个等势面,已知这三个圆的半径之差相等.A、B、C分别是这三个等势面上的点,且在同一条电场线上.A、C两点的电势依次为φA=8V和φC=6V,则B点的电势是( )
如图所示,三个同心圆是同一个点电荷周围的三个等势面,已知这三个圆的半径之差相等.A、B、C分别是这三个等势面上的点,且在同一条电场线上.A、C两点的电势依次为φA=8V和φC=6V,则B点的电势是( )| A. | 一定等于7V | B. | 一定低于7V | C. | 一定高于7V | D. | 无法确定 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 某同学有两卷导线:
某同学有两卷导线:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 点迹密集的地方物体运动的速度较大 | |
| B. | 点迹密集的地方物体运动的速度较小 | |
| C. | 点迹不均匀说明物体做变速运动 | |
| D. | 点迹不均匀说明相邻两点之间的时间间隔不同 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
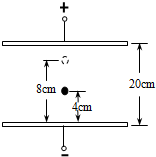 如图所示,水平放置的平行板电容器与一恒定的直流电压相连,两极板间距离d=20cm.距下板4cm处有一质量m=0.01g的不带电小球由静止落下.小球和下极板碰撞间带上了q=1.0×10-8C的电荷,反跳的高度为8cm,这时下板所带电量为Q=2.0×10-6C.如果小球和下板碰撞时没有机械能损失(即速度的大小不变),(取g=10m/s2)试求:
如图所示,水平放置的平行板电容器与一恒定的直流电压相连,两极板间距离d=20cm.距下板4cm处有一质量m=0.01g的不带电小球由静止落下.小球和下极板碰撞间带上了q=1.0×10-8C的电荷,反跳的高度为8cm,这时下板所带电量为Q=2.0×10-6C.如果小球和下板碰撞时没有机械能损失(即速度的大小不变),(取g=10m/s2)试求:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 长为L的导体棒原来不带电,将一带电量为q的点电荷放在棒左端R处,静电力常量为k,如图,当达到静电平衡后棒上感应的电荷在棒内中点处产生的场强的大小为$\frac{kq}{{(R+\frac{L}{2})}^{2}}$,方向水平向左.
长为L的导体棒原来不带电,将一带电量为q的点电荷放在棒左端R处,静电力常量为k,如图,当达到静电平衡后棒上感应的电荷在棒内中点处产生的场强的大小为$\frac{kq}{{(R+\frac{L}{2})}^{2}}$,方向水平向左.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com