在天文学上,太阳的密度是常用的物理量.某同学设想利用小孔成像原理和万有引力定律相结合来探究太阳的密度.探究过程如下:
(1)假设地球上某处对太阳的张角为θ,地球绕太阳公转的周期为T,太阳的半径为R,密度为ρ,质量为M.由三角关系可知,该处距太阳中心的距离为 r=R/sin(θ/2),这一距离也就是地球上该处物体随地球绕太阳公转的轨道半径.于是推得太阳的密度的公式,请你帮他写出推理过程(巳知 地球绕太阳公转的周期为T,万有引力恒量为G):
(2)利用小孔成像原理求θ角
取一个圆筒,在其一端封上厚纸,中间扎小孔,另一端封上一张画有同心圆的薄白纸.相邻同心圆的半径相差1mm,当作测量尺度.把小孔对着太阳,筒壁与光线平行,另一端的纸上就可以看到一个圆光斑,这就是太阳的实像.设光斑圆心到小孔的距离L(足够长)就是筒的长度,那么他还要测出什么量呢?求得θ角的公式是怎样的?
(3)整个探究过程釆用了如下哪些最贴切的科学方法:______
A.类比分析 B.理想实验
C.等效替換 D.控制变量.
【答案】
分析:(1)万有引力提供向心力,从而根据M=ρV,即可求解;
(2)运用几何光学,根据几何关系来确定,即可求解;
(3)对科学研究的方法,要掌握与理解,并学会区分.
解答:解:(1)由 F
向心=F
万得:4π
2m
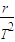
=
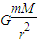
.
T=1年=3.152×10
7s,
M=ρ?

πR
3 太阳的密度:ρ=
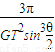
(2)利用小孔成像原理求θ角
由小孔成像原理可知,太阳实像对小孔的张角α与太阳对此处的张角θ为对顶角,
θ=α.还要由薄白纸上的同心圆测出光斑的半径r′.
可测得tan

=
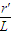
.因为θ角很小tan

≈sin

θ=2arcsin
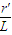
(3)整个探究过程前者釆用了理想实验的逻辑推理,后者使用了等效替换,
故选BC
点评:考查牛顿第二定律,万有引力定律的应用与理解,并掌握几何关系在几何光学的应用.最后理解科学的研究方法.

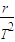 =
=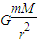 .
. πR3
πR3 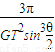
 =
=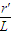 .因为θ角很小tan
.因为θ角很小tan ≈sin
≈sin
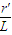


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案