
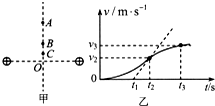
 ��������ͬ�ֵ��ɹ̶��ڹ⻬��Եˮƽ���ϣ������֮��ľ���ΪL�������д�������A��B��C���㣬��ͼ����ʾ��һ�������Ϊ+q������Ϊm��С����C���ɾ�ֹ�ͷţ�t2ʱ�����ͨ��B�㣬t3ʱ�����ͨ��A�㣬���˶���v-tͼ����ͼ����ʾ��t2ʱ��ͼ������б����������̶�����ͬ�ֵ��ɲ����ĵ糡������˵����ȷ���ǣ�������
��������ͬ�ֵ��ɹ̶��ڹ⻬��Եˮƽ���ϣ������֮��ľ���ΪL�������д�������A��B��C���㣬��ͼ����ʾ��һ�������Ϊ+q������Ϊm��С����C���ɾ�ֹ�ͷţ�t2ʱ�����ͨ��B�㣬t3ʱ�����ͨ��A�㣬���˶���v-tͼ����ͼ����ʾ��t2ʱ��ͼ������б����������̶�����ͬ�ֵ��ɲ����ĵ糡������˵����ȷ���ǣ�������| A�� | ��C�㵽A����������� | |
| B�� | B��ij�ǿΪE=$\frac{{m{v_2}}}{{q��{{t_2}-{t_1}}��}}$ | |
| C�� | O��B֮��ľ���Ϊ$\frac{{\sqrt{2}L}}{4}$ | |
| D�� | A��B�����ĵ��Ʋ�UAB=-$\frac{{m��{v_3^2-v_2^2}��}}{2q}$ |
���� ����������ͬ������ɣ��������д����ϵ糡ǿ�ȷ�����O�����д���ָ����ࣻ����Ϊ2C�����˶��������ܵ糡�����ô�C�㵽B���ٵ�A�˶��Ĺ����У�����V-tͼ��֪��B��ļ��ٶ�Ϊ��������������ٶ�����������ٶȼ�С�ļ����˶�������ţ�ٵڶ������жϵ�����ܵ糡����С�仯����ͼ��ٶȱ仯���
��� �⣺A��������������ͬ������ɣ��������д����ϵ糡ǿ�ȷ�����O�����д���ָ����࣬����C�㵽A��Ĺ����е�����С����A����
B����V-tͼ��֪����������B��ļ��ٶ����Ϊ$\frac{{v}_{2}}{{t}_{2}-{t}_{1}}$�����ܵĵ糡�����Ϊma ��E=$\frac{F}{q}=\frac{m{v}_{2}}{{��t}_{2}-{t}_{1}��q}$��B��ȷ��
C�����������B��������0B�Ľ�Ϊ�ȣ���E=$\frac{Kq}{��\frac{L}{2sin��}��^{2}}cos�ȡ�2$=$8\frac{Kq}{{L}^{2}}sin{��}^{2}cos��$=8$\frac{Kq}{{L}^{2}}��1-cos{��}^{2}��cos��$ �������֪��$cos��=\frac{\sqrt{3}}{3}$ʱ��Ӧ��OB֮��ľ���Ϊ$\frac{{\sqrt{2}L}}{4}$����C��ȷ��
D����V-tͼ��֪A��B������ٶȣ��ٸ��ݶ��ܶ����õ糡�����Ĺ���
WBA=$\frac{1}{2}$$��m{v}_{3}^{2}-m{v}_{2}^{2}��$ ${U}_{AB}=\frac{{W}_{AB}}{q}$=-$\frac{{m��{v_3^2-v_2^2}��}}{2q}$��D��ȷ��
��ѡ��BCD
���� ��ȷ����ͬ�ֵ�ɵ糡���ص��ǽⱾ��Ĺؼ�����V-tͼ��ȡ���ٶȡ��ٶȡ����ܵ��������ǽⱾ���ͻ�ƿ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
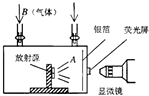 ��ͼ��ʾʵ��װ�ÿ�ʵ��ԭ�Ӻ˵��˹�ת�䣬��װ�õ�������ͨ������Bʱ��ӫ�����Ϲ۲쵽���⣮ͼ������B�ǵ�������ԭ�Ӻ��˹�ת��ĺ˷�Ӧ����ʽ��24He+714N��817O+11H��
��ͼ��ʾʵ��װ�ÿ�ʵ��ԭ�Ӻ˵��˹�ת�䣬��װ�õ�������ͨ������Bʱ��ӫ�����Ϲ۲쵽���⣮ͼ������B�ǵ�������ԭ�Ӻ��˹�ת��ĺ˷�Ӧ����ʽ��24He+714N��817O+11H���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �ڶ�����ʣ�а�ƿ��ˮ��ůˮƿ����һ��ҹ���ڶ����ƿ�ڵ���ľ��ʱ���úܽ������װγ�������Ϊ�����������ߣ�����ѹǿ��� | |
| B�� | һ���������������壬�ȵ������ͣ��ٵ�ѹѹ�����������С����ʼ��� | |
| C�� | �����˶�����Һ����ӵ��˶� | |
| D�� | ����̥������һ���ݹ����У��������ͣ��¶��½� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 һ�˷�յĴ�ϸ���ȵ�U�ιܣ���ˮ�����һ�������Ŀ������ɿ����������壩�������ڿ����¶�Ϊt1=31��ʱ��U������ˮ����ȸߣ���ͼ��ʾ����ʱ��������l1=8cm���������ѹǿ��Ϊp0=76cmHg����
һ�˷�յĴ�ϸ���ȵ�U�ιܣ���ˮ�����һ�������Ŀ������ɿ����������壩�������ڿ����¶�Ϊt1=31��ʱ��U������ˮ����ȸߣ���ͼ��ʾ����ʱ��������l1=8cm���������ѹǿ��Ϊp0=76cmHg�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
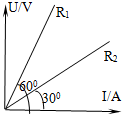
| A�� | 1��3 | B�� | 3��1 | C�� | 1��$\sqrt{3}$ | D�� | $\sqrt{3}$��1 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 6m/s | B�� | 2$\sqrt{3}$m/s | C�� | 3m/s | D�� | 3$\sqrt{3}$m/s |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
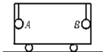 ��ͼ��ʾ������ȫ��ͬ������С��A��B���ó�L=0.4m��ϸ��������v=2m/s���������˶���С��������������С��ǰ��ڽӴ�������ij��ԭ��С��ͻȻֹͣ�˶�����ʱ���ߵ�����֮��FB��FAΪ��g=10m/s2����������
��ͼ��ʾ������ȫ��ͬ������С��A��B���ó�L=0.4m��ϸ��������v=2m/s���������˶���С��������������С��ǰ��ڽӴ�������ij��ԭ��С��ͻȻֹͣ�˶�����ʱ���ߵ�����֮��FB��FAΪ��g=10m/s2����������| A�� | 1��1 | B�� | 1��2 | C�� | 1��3 | D�� | 1��4 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��˹�ط����˵����Ĵ�ЧӦ���ܽ���˵�Ÿ�Ӧ���� | |
| B�� | ����ѧ�У��ʵ㡢ƽ���ٶȡ���������������������Чֵ���������Ķ�������˵�Ч�����˼�뷽�� | |
| C�� | ������ζ��ɣ���Ӧ�����Ĵų�����Ҫ�谭ԭ�ų��Ĵ�ͨ���ı仯 | |
| D�� | ��Ȧ�Ĵ�ͨ������Ȧ�������أ���Ȧ�в����ĸ�Ӧ�綯��Ҳ����Ȧ�������� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com