
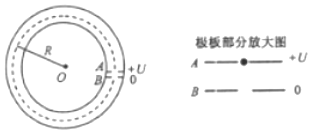
 如图所示为一种获得高能粒子的装置.环形区域内存在垂直纸面向外、大小可调节的匀强磁场.质量为m、电量为+q的粒子在环中做半径为R的圆周运动.A、B为两块中心开有小孔的极板,板间距为d.A、B板原来电势都为零,每当粒子飞经A板向B板运动时,A板电势升高为+U,B板电势仍保持为零,粒子在两板间电场中得到加速.每当粒子离开B板时,A板电势又降为零.粒子在电场一次次加速下动能不断增大,而绕行半径不变.粒子的重力忽略不计.
如图所示为一种获得高能粒子的装置.环形区域内存在垂直纸面向外、大小可调节的匀强磁场.质量为m、电量为+q的粒子在环中做半径为R的圆周运动.A、B为两块中心开有小孔的极板,板间距为d.A、B板原来电势都为零,每当粒子飞经A板向B板运动时,A板电势升高为+U,B板电势仍保持为零,粒子在两板间电场中得到加速.每当粒子离开B板时,A板电势又降为零.粒子在电场一次次加速下动能不断增大,而绕行半径不变.粒子的重力忽略不计.分析 (1)由动能定理求出第一次经电场加速后的速度.
(2)由洛仑兹力提供向心力求出半径公式r=$\frac{mv}{qB}$,由于半径不变,但速度不断增大,则只有磁感应强度B也要不断增大,才能保证半径不变,求出绕行第n圈时的速度大小,由洛仑兹力提供向心力就能求得绕行第n圈时所需的磁感应强度.
(3)分别求出粒子在磁场中第1圈、第2圈…第n圈绕行所用时间,相加之后再加上在电场中n次加速的总时间,就得到粒子绕行n圈r所需总时间tn总
解答 解:(1)粒子从静止开始第一次加速时,由动能定理$qU=\frac{1}{2}m{{v}_{1}}^{2}$
解得:v1=$\sqrt{\frac{2qU}{m}}$
(2)粒子绕行第n圈时,nqU=$\frac{1}{2}m{{v}_{n}}^{2}$
粒子受到的洛仑兹力提供向心力,qvnBn=$\frac{m{{v}_{n}}^{2}}{R}$
解得:Bn=$\frac{1}{R}\sqrt{\frac{2nmU}{q}}$
(3)粒子在磁场中绕行第n圈的周期Tn=$\frac{2πR}{{v}_{n}}=\frac{2πm}{q{B}_{n}}$
粒子在磁场中绕行第1圈所用时间t磁1=$\frac{2πm}{q{B}_{1}}$,B1=$\frac{1}{R}\sqrt{\frac{2×1mU}{q}}$
粒子在磁场中绕行第2圈所用时间t磁2=$\frac{2πm}{q{B}_{2}}$,B2=$\frac{1}{R}\sqrt{\frac{2×2mU}{q}}$
粒子在磁场中绕行第3圈所用时间t磁3=$\frac{2πm}{q{B}_{3}}$,B3=$\frac{1}{R}\sqrt{\frac{2×3mU}{q}}$
余次类推,粒子在磁场中绕行第n圈所用时间t磁n=$\frac{2πm}{q{B}_{n}}$,Bn=$\frac{1}{R}\sqrt{\frac{2×nmU}{q}}$
解得:t磁n总=t磁1+t磁2+t磁3+…+t磁n=$2πR\sqrt{\frac{m}{2qU}}(1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+…+\frac{1}{\sqrt{n}})$
设粒子在电场中绕行n圈所用总时间为t电n总,有a=$\frac{qU}{dm}$
nd=$\frac{1}{2}a{{t}_{电n总}}^{2}$
则粒子绕行n圈所需的总时间
tn总=t磁n总+t电n总=$2πR\sqrt{\frac{m}{2qU}}(1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+…+\frac{1}{\sqrt{n}})$+$\sqrt{\frac{2nm{d}^{2}}{qU}}$
答:(1)设t=0时,粒子静止在A板小孔处,在电场作用下加速.粒子第一次穿过B板时速度的大小v1为$\sqrt{\frac{2qU}{m}}$.
(2)为使粒子始终保持在半径为R的圆轨道上运动,磁场必须周期性递增.粒子绕行第n圈时磁感应强度的大小Bn为$\frac{1}{R}\sqrt{\frac{2nmU}{q}}$.
(3)粒子绕行n圈所需的总时间tn总为$2πR\sqrt{\frac{m}{2qU}}(1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+…+\frac{1}{\sqrt{n}})$+$\sqrt{\frac{2nm{d}^{2}}{qU}}$.
点评 本题的不同之处是在回旋加速器的基础上进行改装的加速器,只是粒子做匀速圆周运动的半径始终为盒的半径R不变,但由于每经过同一地点均要加速粒子,所以粒子的速度要增加,要保证半径不变则要每次的磁感应强度的大小也相应的增大.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中物理 来源: 题型:多选题
| A. | 原子核发生一次β衰变,该原子外层就失去一个电子 | |
| B. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减小,但原子的能量增大 | |
| C. | 比结合能越大,原子核中核子结合得越牢固,原子核越稳定 | |
| D. | 一束光照射到某种金属上不能发生光电效应,可能是因为这束光的光强太小 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
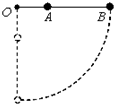 如图所示,长为3l的轻质细杆一端可绕O点自由转动,杆上距O点l和3l处分别固定质量均为m的小球A、B.现将细杆拉至水平,并由静止释放,忽略一切摩擦及空气阻力,则当杆由水平转到竖直位置过程中( )
如图所示,长为3l的轻质细杆一端可绕O点自由转动,杆上距O点l和3l处分别固定质量均为m的小球A、B.现将细杆拉至水平,并由静止释放,忽略一切摩擦及空气阻力,则当杆由水平转到竖直位置过程中( )| A. | 此过程A球机械能守恒,B球机械能守恒 | |
| B. | 此过程A球机械能减少,B球机械能增加 | |
| C. | 当杆到达竖直位置时,球B的速度大小为2$\sqrt{\frac{gl}{5}}$ | |
| D. | 当杆达到竖直位置时,OA段杆对球的拉力大小为$\frac{26}{5}$mg |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
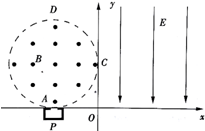 如图所示,在第一象限内有沿y轴负方向的电场强度大小为E的匀强磁场.在第二象限中,半径为R的圆形区域内存在垂直纸面向外的匀强磁场.圆形区域与x、y轴分别相切于A、C两点;在A点正下方有一个粒子源P,P可以向x轴上方各个方向射出速度大小均为v0,质量为m、电量为+q的带电粒子(重力不计,不计粒子间的相互作用),其中沿y轴正方向射出的带电粒子刚好从C点垂直于y轴进入电场
如图所示,在第一象限内有沿y轴负方向的电场强度大小为E的匀强磁场.在第二象限中,半径为R的圆形区域内存在垂直纸面向外的匀强磁场.圆形区域与x、y轴分别相切于A、C两点;在A点正下方有一个粒子源P,P可以向x轴上方各个方向射出速度大小均为v0,质量为m、电量为+q的带电粒子(重力不计,不计粒子间的相互作用),其中沿y轴正方向射出的带电粒子刚好从C点垂直于y轴进入电场查看答案和解析>>
科目:高中物理 来源: 题型:选择题
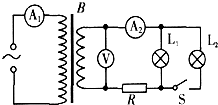 图中B为理想变压器,接在交变电压有效值保持不变的电源上.指示灯L1和L2完全相同(其阻值均恒定不变),R是一个定值电阻,电压表、电流表都为理想电表.开始时开关S是闭合的,当S断开后,下列说法正确的是( )
图中B为理想变压器,接在交变电压有效值保持不变的电源上.指示灯L1和L2完全相同(其阻值均恒定不变),R是一个定值电阻,电压表、电流表都为理想电表.开始时开关S是闭合的,当S断开后,下列说法正确的是( )| A. | 电流表A2的示数变大 | B. | 电流表A1的示数变小 | ||
| C. | 电压表的示数变大 | D. | 灯泡L1的亮度变暗 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
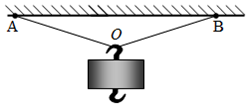 某同学提出了仅运用一个已知质量为m的钩码和一把米尺进行测量的方案.首先,他把钩码直接悬挂在这种棉线上,结果棉线没有断,而且没有发生明显伸长.然后该同学利用如图的装置,得出了该棉线能承受的最大拉力(细线两端点A、B始终位于同一水平线).请你根据该同学已具有的上述器材,回答下列问题(已知重力加速度为g):
某同学提出了仅运用一个已知质量为m的钩码和一把米尺进行测量的方案.首先,他把钩码直接悬挂在这种棉线上,结果棉线没有断,而且没有发生明显伸长.然后该同学利用如图的装置,得出了该棉线能承受的最大拉力(细线两端点A、B始终位于同一水平线).请你根据该同学已具有的上述器材,回答下列问题(已知重力加速度为g):查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 如图所示,两个质量各为m1和m2的小物块A和B,分别系在一条跨过定滑轮的软绳两端,已知m1>m2,现要利用此装置验证机械能守恒定律.
如图所示,两个质量各为m1和m2的小物块A和B,分别系在一条跨过定滑轮的软绳两端,已知m1>m2,现要利用此装置验证机械能守恒定律.查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 为了测定一根轻弹簧压缩到最短时具有的弹性势能的大小,可以将弹簧固定在一带有凹槽轨道的一端,并将轨道固定在水平桌面边缘上,如图所示,用钢球将弹簧压缩至最短,而后突然释放,钢球将沿轨道飞出桌面,实验时:
为了测定一根轻弹簧压缩到最短时具有的弹性势能的大小,可以将弹簧固定在一带有凹槽轨道的一端,并将轨道固定在水平桌面边缘上,如图所示,用钢球将弹簧压缩至最短,而后突然释放,钢球将沿轨道飞出桌面,实验时:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 40Hz | B. | $\frac{1}{40}$Hz | C. | $\frac{3}{2}$Hz | D. | $\frac{2}{3}$Hz |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com