
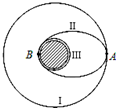
 “嫦娥一号”在西昌卫星发射中心发射升空,准确进入预定轨道.随后,“嫦娥一号”经过变轨和制动成功进入环月轨道.如图所示,阴影部分表示月球,设想飞船在圆形轨道Ⅰ上作匀速圆周运动,在圆轨道Ⅰ上飞行n圈所用时间为t到达A点时经过暂短的点火变速,进入椭圆轨道Ⅱ,在到达轨道Ⅱ近月点B点时再次点火变速,进入近月圆形轨道Ⅲ,而后飞船在轨道Ⅲ上绕月球作匀速圆周运动,在圆轨道Ⅲ上飞行n圈所用时间为$\frac{t}{8}$.不考虑其它星体对飞船的影响,求:
“嫦娥一号”在西昌卫星发射中心发射升空,准确进入预定轨道.随后,“嫦娥一号”经过变轨和制动成功进入环月轨道.如图所示,阴影部分表示月球,设想飞船在圆形轨道Ⅰ上作匀速圆周运动,在圆轨道Ⅰ上飞行n圈所用时间为t到达A点时经过暂短的点火变速,进入椭圆轨道Ⅱ,在到达轨道Ⅱ近月点B点时再次点火变速,进入近月圆形轨道Ⅲ,而后飞船在轨道Ⅲ上绕月球作匀速圆周运动,在圆轨道Ⅲ上飞行n圈所用时间为$\frac{t}{8}$.不考虑其它星体对飞船的影响,求:分析 (1)根据万有引力提供圆周运动向心力求得中心天体质量,再根据密度公式求得密度;
(2)根据开普勒行星定律由半长轴的关系求得周期,从远月点飞到近月点所用时间为椭圆轨道的$\frac{1}{2}$周期;
(3)相距最近时,两飞船中运得快的比运动得慢的多绕月飞行n周,根据角速度关系求解所用时间即可.
解答 解:(1)在圆轨道Ⅲ上的周期:
T3=$\frac{t}{8n}$…①
由万有引力提供向心力有:
$G\frac{mM}{{R}^{2}}=mR\frac{4{π}^{2}}{{T}_{3}^{2}}$…②
又:M=$ρ•\frac{4}{3}π{R}^{3}$…③
联立得:$ρ=\frac{3π}{G{T}_{3}^{2}}$=$\frac{192π{n}^{2}}{G{t}^{2}}$…④
(2)设飞船在轨道I上的运动周期为T1,在轨道I有:$G\frac{mM}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}_{1}^{2}}$…⑤
又:${T}_{1}=\frac{t}{n}$…⑥
联立①②⑤⑥得:r=4R
设飞船在轨道II上的运动周期T2,而轨道II的半长轴为:$b=\frac{r+R}{2}$=2.5R…⑦
根据开普勒定律得:
$\frac{{T}_{2}^{2}}{{(2.5R)}^{3}}=\frac{{T}_{3}^{2}}{{(4R)}^{3}}$…⑧
可解得:T2=0.494T3
所以飞船从A到B的飞行时间为:$t=\frac{{T}_{2}}{2}=\frac{0.247t}{n}$
(3)设飞船在轨道I上的角速度为ω1、在轨道III上的角速度为ω3,有:${ω}_{1}=\frac{2π}{{T}_{1}}$
所以${ω}_{3}=\frac{2π}{{T}_{3}}$
设飞飞船再经过t时间相距最近,有:
ω3t′-ω1t′=2mπ
所以有:t=$\frac{mt}{7n}$(m=1,2,3…)
答:(1)月球的平均密度是$\frac{192π{n}^{2}}{G{t}^{2}}$.
(2)飞船从轨道Ⅱ上远月点A运动至近月点B所用的时间为$\frac{0.247t}{n}$.
(3)则经$\frac{mt}{7n}$(m=1,2,3…),他们又会相距最近.
点评 本题主要考查万有引力定律的应用,开普勒定律的应用.同时根据万有引力提供向心力列式计算.


科目:高中物理 来源: 题型:选择题

| A. | 小球过最高点时,绳子张力不可以为0 | |
| B. | 小球过最高点时的最小速度是$\sqrt{gR}$ | |
| C. | 小球恰巧可以作圆周运动过最高点时处于完全失重状态,此时不受重力 | |
| D. | 小球过最高点时,绳子对小球的作用力可以与所受的重力方向相反 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | Y粒子为β粒子 | |
| B. | 若${\;}_{53}^{131}$I的半衰期大约是8天,取4个碘原子核,经16天就只剩下1个碘原子核了 | |
| C. | 生成的${\;}_{54}^{131}$Xe处于激发态,放射γ射线.γ射线的穿透能力最强,电离能力也最强 | |
| D. | 如果放射性物质碘131处于化合态,也不会对放射性产生影响 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,质量mB=3.5kg的物体B通过一轻弹簧固连在地面上,弹簧的劲度系数k=100N/m.一轻绳一端与物体B连接,绕过无摩擦的两个轻质小定滑轮O1、O2后,另一端与套在光滑直杆顶端的、质量mA=1.6kg的小球A连接.已知斜杆固定,杆长L为0.8m,且与水平面的夹角θ=37°.初始时使小球A静止不动,与A端相连的绳子保持水平,此时绳子中的张力F为45N.已知AO1=0.5m,g取10m/s2.现将小球A从静止释放,则:
如图所示,质量mB=3.5kg的物体B通过一轻弹簧固连在地面上,弹簧的劲度系数k=100N/m.一轻绳一端与物体B连接,绕过无摩擦的两个轻质小定滑轮O1、O2后,另一端与套在光滑直杆顶端的、质量mA=1.6kg的小球A连接.已知斜杆固定,杆长L为0.8m,且与水平面的夹角θ=37°.初始时使小球A静止不动,与A端相连的绳子保持水平,此时绳子中的张力F为45N.已知AO1=0.5m,g取10m/s2.现将小球A从静止释放,则:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 保持两小球的材料不变,使两小球的半径和距离均减少为原来的$\frac{1}{2}$ | |
| B. | 保持两小球的材料和距离不变,让两小球的半径变为原来的$\frac{1}{2}$ | |
| C. | 保持两小球的材料和半径不变,让两小球间的距离变为原来的2倍 | |
| D. | 保持两物体的材料不变,让两物体的半径和距离均变为原来的2倍 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
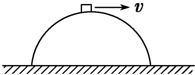 如图所示,小物块位于固定在地面的半径为R的半球的顶端,若给小物块以水平的初速度v0时物块对半球刚好无压力,则下列说法正确的是( )
如图所示,小物块位于固定在地面的半径为R的半球的顶端,若给小物块以水平的初速度v0时物块对半球刚好无压力,则下列说法正确的是( )| A. | 小物块将沿着球面运动一段时间后落地 | |
| B. | 小物块立即离开球面做平抛运动 | |
| C. | 小物块落地时水平位移为$\sqrt{2}$R | |
| D. | 物块落地时速度的方向与地面成45°角 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
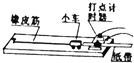 如图所示,在进行探究做功与速度关系的实验中,每次实验结束后要通过探究纸带上点来确定每次小车运动的最大速度,关于最大速度的测算描述正确的是( )
如图所示,在进行探究做功与速度关系的实验中,每次实验结束后要通过探究纸带上点来确定每次小车运动的最大速度,关于最大速度的测算描述正确的是( )| A. | 利用开始纸带上打出的较为密集的点进行测算 | |
| B. | 利用中段纸带上打出的点进行测算 | |
| C. | 利用纸带上打下的从开始到最后的所有点进行测算 | |
| D. | 利用纸带上打出的间隔较为均匀分布的点进行测算 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com