
分析 万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}r$,和在地球表面的物体受到的重力等于万有引力$mg=G\frac{Mm}{{R}^{2}}$,可以解得组合体离地面的高度,根据线速度与轨道半径和周期的关系可以计算出速度大小.根据能量守恒结合线速度的表达式计算动机做功前神舟十号飞船所在的高度.
解答 解:(1)组合体绕地球做圆周运动,万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}r$
又因为在地球表面的物体受到的重力等于万有引力$mg=G\frac{Mm}{{R}^{2}}$
解得$r=\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$
因为r=h+R
所以组合体离地面的高度为h=r-R=$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}-R$
运行的速度为v=$\frac{2πr}{T}$=$\frac{2π}{T}\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$=$\root{3}{\frac{2πg{R}^{2}}{T}}$
(2)根据万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$,得$v=\sqrt{\frac{GM}{r}}$,
神舟十号飞船在较低的轨道上做离心运动到高轨道上与天宫一号对接,轨道高度增加,速度减小,即动能减小.
根据能量守恒定律可知,减少的动能为△Ek=E-W
即$\frac{1}{2}m{v}^{2}-\frac{1}{2}m(\root{3}{\frac{2πg{R}^{2}}{T}})^{2}=E-W$
因为$v=\sqrt{\frac{GM}{r}}$=$\sqrt{\frac{g{R}^{2}}{R+H}}$
所以$\frac{1}{2}m\frac{g{R}^{2}}{R+H}-\frac{1}{2}m{(\root{3}{\frac{2πg{R}^{2}}{T}})}^{2}=E-W$
解得H=$\frac{g{R}^{2}}{\frac{2(E-W)}{m}-({\frac{2πg{R}^{2}}{T})}^{\frac{2}{3}}}-R$
答:(1)组合体离地面的高度为$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}-R$,速度大小为$\root{3}{\frac{2πg{R}^{2}}{T}}$;
(2)发动机做功前,神舟十号飞船所在的高度是$\frac{g{R}^{2}}{\frac{2(E-W)}{m}-({\frac{2πg{R}^{2}}{T})}^{\frac{2}{3}}}-R$.
点评 本题关键是要掌握万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}r$和在地球表面的物体受到的重力等于万有引力$mg=G\frac{Mm}{{R}^{2}}$这两个关系,并且要能够根据题意选择恰当的向心力的表达式.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中物理 来源: 题型:解答题
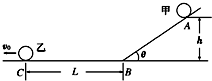 如图所示,小球甲从倾角θ=30°的光滑斜面上高h=5cm的A点由静止释放,小球沿斜面向下做匀加速直线运动,下滑的加速度大小为5m/s2,同时小球乙自C点以速度v0沿光滑水平面向左匀速运动,C点与斜面底端B处的距离L=0.4m.设甲到达B点时速度为VB,且甲滑下后能沿斜面底部的光滑小圆弧平稳地朝乙追去此后速度始终为VB,甲释放后经过t=1s刚好追上乙,求:
如图所示,小球甲从倾角θ=30°的光滑斜面上高h=5cm的A点由静止释放,小球沿斜面向下做匀加速直线运动,下滑的加速度大小为5m/s2,同时小球乙自C点以速度v0沿光滑水平面向左匀速运动,C点与斜面底端B处的距离L=0.4m.设甲到达B点时速度为VB,且甲滑下后能沿斜面底部的光滑小圆弧平稳地朝乙追去此后速度始终为VB,甲释放后经过t=1s刚好追上乙,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | E=$\frac{GMm}{2}$($\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$) | B. | E=GMm($\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$) | C. | E=$\frac{GMm}{3}$($\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$) | D. | E=$\frac{2GMm}{3}$($\frac{1}{{r}_{2}}$-$\frac{1}{{r}_{1}}$) |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
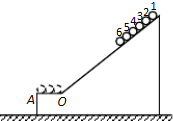 斜面体上开有凹槽,槽内紧挨放置六个半径均为r的相同刚性小球,各球编号如图,斜面与水平轨道OA平滑连接,OA长度为6r.现将六个小球由静止同时释放,小球离开A点后均做平抛运动,不计一切摩擦.则在各小球运动过程中,下列说法正确的是( )
斜面体上开有凹槽,槽内紧挨放置六个半径均为r的相同刚性小球,各球编号如图,斜面与水平轨道OA平滑连接,OA长度为6r.现将六个小球由静止同时释放,小球离开A点后均做平抛运动,不计一切摩擦.则在各小球运动过程中,下列说法正确的是( )| A. | 球6的机械能守恒 | B. | 球6在OA段机械能增大 | ||
| C. | 球6的水平射程最大 | D. | 有三个球落地点位置相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,质量为m、电荷量为+q的塑料小球从小孔S处无初速度地进入一个区域足够大的匀强磁场中,磁感应强度为B,求:
如图所示,质量为m、电荷量为+q的塑料小球从小孔S处无初速度地进入一个区域足够大的匀强磁场中,磁感应强度为B,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 0.8T | B. | 0.4T | C. | 0.2T | D. | 0.1T |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com