
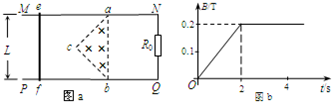
分析 (1)根据法拉第电磁感应定律可得感应电动势,根据欧姆定律求解电流强度,根据焦耳定律计算产生的焦耳热;
(2)根据E=BLv求解电动势,根据安培力的计算公式和共点力的平衡条件求解外力F的最大值;求出在时间t时切割磁感线的长度,根据e=B0lv0解得电动势e与时间t的关系.
解答 解:(1)导体棒进入磁场前,闭合回路efR0中感应电动势恒定,设为E1,电流为I1,有感应电流的时间t1=2s,三角形区域的面积为S,电阻R0产生的热量为Q1,则
面积S=$\frac{1}{2}L•\frac{1}{2}L=\frac{1}{4}{L}^{2}$=0.01m2,
根据法拉第电磁感应定律可得感应电动势:E1=$\frac{△B}{△t}•S$=0.001V,
感应电流:I1=$\frac{{E}_{1}}{{R}_{0}}$=0.005A;
根据焦耳定律可得:Q1=${I}_{1}^{2}{R}_{0}{t}_{1}$
解得:Q1=1.0×10-5J;
(2)t0=4s,导体棒进入磁场,当到达位置ab时,设电动势为E2,电流为I2,安培力最大为F2,外力F的最大值为Fm,则
E2=B0Lv0=8×10-3V,
电流:I2=$\frac{{E}_{2}}{{R}_{0}}=0.04A$,
最大安培力F2=B0I2L=1.6×10-3N,
外力F的最大值为Fm=F2,
则F2=Fm=1.6×10-3N;
设导体棒通过三角形区域abc区域的时间为t0,设在时间t,切割磁感线的长度为l,则t0=$\frac{\frac{L}{2}}{{v}_{0}}$=0.5s
l=2v0(t-4)(4s≤t≤4.5s)
则e=B0lv0,
解得电动势e与时间t的关系式为:e=0.016t-0.064 V (4s≤t≤4.5s).
答:(1)导体棒进入磁场前,电阻R0产生的热量为1.0×10-5J;
(2)导体棒通过三角形区域abc过程中,外力F的最大值为1.6×10-3N;导体棒中的电动势e与时间t的关系式为e=0.016t-0.064 V (4s≤t≤4.5s).
点评 对于电磁感应问题研究思路常常有两条:一条从力的角度,重点是分析安培力作用下导体棒的平衡问题,根据平衡条件列出方程;另一条是能量,分析涉及电磁感应现象中的能量转化问题,根据动能定理、功能关系等列方程求解.


科目:高中物理 来源: 题型:计算题
 如图所示为四旋翼无人机,它是一种能够垂直起降的小型遥控飞行器,目前正得到越来越广泛的应用.一架质量m=1kg的无人机,其动力系统所能提供的最大升力F=16N,无人机上升过程中最大速度为6m/s.若无人机从地面以最大升力竖直起飞,打到最大速度所用时间为3s,假设无人机竖直飞行时所受阻力大小不变.(g取10m/s2).求:
如图所示为四旋翼无人机,它是一种能够垂直起降的小型遥控飞行器,目前正得到越来越广泛的应用.一架质量m=1kg的无人机,其动力系统所能提供的最大升力F=16N,无人机上升过程中最大速度为6m/s.若无人机从地面以最大升力竖直起飞,打到最大速度所用时间为3s,假设无人机竖直飞行时所受阻力大小不变.(g取10m/s2).求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,质量M=4kg的空箱子,静止放在光滑的水平面上,箱子中有一个质量m=2kg的铁块,铁块与箱子的左端ab壁相距x=2m,它一旦与ab壁接触后就不会再分开,铁块与箱底间的动摩擦因数为0.1,现用水平向右的恒力F=10N作用于箱子,在2s末立即撤去作用力F,g=10m/s2,则:
如图所示,质量M=4kg的空箱子,静止放在光滑的水平面上,箱子中有一个质量m=2kg的铁块,铁块与箱子的左端ab壁相距x=2m,它一旦与ab壁接触后就不会再分开,铁块与箱底间的动摩擦因数为0.1,现用水平向右的恒力F=10N作用于箱子,在2s末立即撤去作用力F,g=10m/s2,则:查看答案和解析>>
科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 某同学利用电压表和定值电阻测蓄电池电源的电动势和内阻.
某同学利用电压表和定值电阻测蓄电池电源的电动势和内阻.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
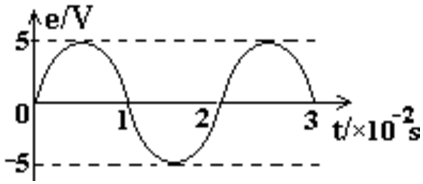 一交流发电机产生的感应电动势随时间变化的图象如图所示.求:
一交流发电机产生的感应电动势随时间变化的图象如图所示.求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 若一边长为a质量为m木块放在底面为正方形(边长为$\sqrt{2}$a)的盛水足够深的长方体容器中,开始时,木块静止,有一半没入水中,水面距容器底的距离为2a,如图所示,现用力F将木块缓慢地压到容器底部,不计摩擦,求这一过程中压力做的功.
若一边长为a质量为m木块放在底面为正方形(边长为$\sqrt{2}$a)的盛水足够深的长方体容器中,开始时,木块静止,有一半没入水中,水面距容器底的距离为2a,如图所示,现用力F将木块缓慢地压到容器底部,不计摩擦,求这一过程中压力做的功.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,光滑的水平地面上有一辆平板上,车上有一个人.原来车和人都静止.当人从左向右行走的过程中,下列说法正确的是( )
如图所示,光滑的水平地面上有一辆平板上,车上有一个人.原来车和人都静止.当人从左向右行走的过程中,下列说法正确的是( )| A. | 人和车组成的系统动量不守恒 | B. | 人和车组成的系统机械能守恒 | ||
| C. | 人行车行,人停车停 | D. | 人和车的速度方向相同 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com