
 (2012?房山区模拟)如图所示,质量为m的小物块以水平速度v0滑上原来静止在光滑水平面上质量为M的小车上,物块与小车间的动摩擦因数为μ,小车足够长.求:
(2012?房山区模拟)如图所示,质量为m的小物块以水平速度v0滑上原来静止在光滑水平面上质量为M的小车上,物块与小车间的动摩擦因数为μ,小车足够长.求: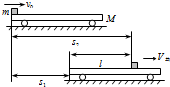 解:物块滑上小车后,受到向后的摩擦力而做减速运动,小车受到向前的摩擦力而做加速运动,因小车足够长,最终物块与小车相对静止,如图所示.由于“光滑水平面”,系统所受合外力为零,故满足动量守恒定律.
解:物块滑上小车后,受到向后的摩擦力而做减速运动,小车受到向前的摩擦力而做加速运动,因小车足够长,最终物块与小车相对静止,如图所示.由于“光滑水平面”,系统所受合外力为零,故满足动量守恒定律.| mv0 |
| M+m |
| mv0 |
| M+m |
| Mv0 |
| μg(M+m) |
| 1 |
| 2 |
| V | 2 共 |
| 1 |
| 2 |
| v | 2 0 |
M
| ||
| 2μ(M+m)g |
| mv0 |
| M+m |
| Mv0 |
| μg(M+m) |
M
| ||
| 2μ(M+m)g |


科目:高中物理 来源: 题型:
 (2012?房山区一模)在竖直平面内有一个粗糙的
(2012?房山区一模)在竖直平面内有一个粗糙的| 1 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com