
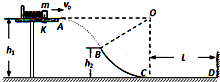
 如图所示,在距水平地面高h1=1.2m的光滑水平台面上,一个质量m=1kg的小物块压缩弹簧后被锁扣K锁住,储存的弹性势能为Ep,现打开锁扣K,物块与弹簧分离后将以一定的水平速度向右滑离平台,并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC.已知B点距水平地面的高h2=0.6m,圆弧轨道BC的圆心为O,0点与A点等高,C点的切线水平,并与水平地面上长为L=2.8m的粗糙直轨道CD平滑连接,小物块沿轨道BCD运动并与右边的竖直墙壁会发生碰撞,重力加速度g=10m/s2,空气阻力忽略不计.试求:
如图所示,在距水平地面高h1=1.2m的光滑水平台面上,一个质量m=1kg的小物块压缩弹簧后被锁扣K锁住,储存的弹性势能为Ep,现打开锁扣K,物块与弹簧分离后将以一定的水平速度向右滑离平台,并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC.已知B点距水平地面的高h2=0.6m,圆弧轨道BC的圆心为O,0点与A点等高,C点的切线水平,并与水平地面上长为L=2.8m的粗糙直轨道CD平滑连接,小物块沿轨道BCD运动并与右边的竖直墙壁会发生碰撞,重力加速度g=10m/s2,空气阻力忽略不计.试求:分析 (1)小物块做平抛运动,根据高度求出平抛运动的时间,由速度公式求得小物块到达B点时竖直方向的速度,运用运动的分解法求解物块运动到B的瞬时速度vB;小物块从释放到运动达到A的过程中,运用机械能守恒定律求弹簧开始时储存的弹性势能大小.
(2)先根据功能关系列式求解C点的速度,在C点,支持力和重力的合力提供向心力,根据牛顿第二、第三定律列式求解;
(3)根据能量守恒列出能量等式解决问题.由于物块的末位置不确定,要考虑物块可能的滑过的路程.
解答 解:(1)小物块由A运动到B的过程中做平抛运动,在竖直方向上根据自由落体运动规律可知,小物块由A运动到B的时间为:
t=$\sqrt{\frac{2({h}_{1}-{h}_{2})}{g}}$=$\frac{\sqrt{3}}{5}$s
到达B点时竖直方向的速度大小为:
vBy=gt=2$\sqrt{3}$m/s
根据图中几何关系可知,
cos∠BOC=$\frac{{h}_{1}-{h}_{2}}{{h}_{1}}$
解得:cos∠BOC=60°
所以,vB与水平方向的夹角为60°
根据平抛运动规律有:
vB=$\frac{{v}_{By}}{sin60°}$=4m/s
v0=vBcos60°=2m/s
小物块从释放到运动达到A的过程中,机械能守恒,有
EP=$\frac{1}{2}$mv02=2J
(2)对小球从A到C的运动过程,根据能的转化与守恒可知,
Ep+mgh1=$\frac{1}{2}$mvC2,
解得:vC=2$\sqrt{7}$m/s,
对小球在圆弧轨道C点应用牛顿运动定律:
Nc-mg=m$\frac{{v}_{C}^{2}}{R}$
解得 Nc≈33.3N
根据牛顿第三定律知,物块在圆弧轨道BC上滑到C时对轨道压力 N=Nc≈33.3N
(3)依据题意知,
①μ的最大值对应的是物块撞墙前瞬间的速度刚好等于零,根据能量关系有:
mgh1+Ep=μmgL 代入数据解得:μ=$\frac{1}{2}$
②对于μ的最小值求解,首先应判断物块第一次碰墙后反弹,能否沿圆轨道滑离B点,设物块碰前在D处的速度为v2,由能量关系有:
mgh1+Ep=μmgL+$\frac{1}{2}$mv22
第一次碰墙后返回至C处的动能为:EkC=$\frac{1}{8}$mv22-μmgL 可知即使μ=0,有:
$\frac{1}{2}$mv22=14J,$\frac{1}{8}$mv22=3.5J<mgh2=6J,小物块不可能返滑至B点
故μ的最小值对应着物块撞后回到圆轨道最高某处,又下滑经C恰好至D点停止,因此有:
$\frac{1}{8}$mv22=2μmgL,联立mgh1+Ep=μmgL+$\frac{1}{2}$mv22,解得:μ=$\frac{1}{18}$
综上可知满足题目条件的动摩擦因数μ值:$\frac{1}{18}$<μ≤$\frac{1}{2}$
答:(1)小物块运动到B的瞬时速度vB大小为4m/s,弹簧开始时储存的弹性势能大小2J.
(2)物块在圆弧轨道BC上滑到C时对轨道压力为33.3N.
(3)小物块与轨道CD之间的动摩擦因数μ应该满足的条件是:$\frac{1}{18}$<μ≤$\frac{1}{2}$.
点评 做物理问题应该先清楚研究对象的运动过程,根据运动性质利用物理规律解决问题;关于能量守恒的应用,要清楚物体运动过程中能量的转化.


科目:高中物理 来源: 题型:选择题
| A. | $\frac{25}{9}F$ | B. | $\frac{9}{25}F$ | C. | $\frac{16}{9}F$ | D. | $\frac{9}{16}F$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 摩擦力的方向总是和物体运动方向或运动趋势方向相反 | |
| B. | 相互接触的物体间正压力增大,摩擦力不一定增大 | |
| C. | 物体受到静摩擦力大小和接触面材料及其粗糙程度无关 | |
| D. | 运动的物体可能受到静摩擦力 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 该同学的位移为200m | B. | 该同学的路程为200m | ||
| C. | 平均速度为8m/s | D. | 平均速率为8m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 若v0>$\sqrt{gH}$,两物体相遇时,B正在下降途中 | |
| B. | v0=$\sqrt{gH}$,两物体在地面相遇 | |
| C. | 若$\sqrt{\frac{gH}{2}}$<v0<$\sqrt{gH}$,两物体相遇时B物正在空中下落 | |
| D. | 若v0=$\sqrt{\frac{gH}{2}}$,则两物体在地面相遇 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 电荷量 e 的数值最早是由美国物理学家密立根测得的 | |
| B. | 奥斯特研究并总结出电流对电流的作用规律 | |
| C. | 安培研究并总结出计算电热的公式 | |
| D. | 库仑在前人工作的基础上,通过实验研究确认了真空中任何两个带电体之间的相互作用力的规律 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com