
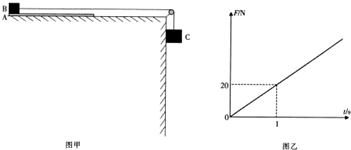
分析 (1)对ABC整体研究,假设一起运动,根据牛顿第二定律求出加速度,再隔离分析求出AB间的摩擦力,与最大静摩擦力比较,判断是否保持相对静止.
(2)通过整体隔离分析得出A与B发生相对滑动,根据牛顿第二定律分别求出A、B的加速度,结合运动学公式进行求解.
(3)通过牛顿第二定律得出C加速度的表达式,作出图线,结合图线与时间轴围成的面积进行求解.
解答 解:(1)设ABC一起运动,以ABC为系统,根据牛顿第二定律: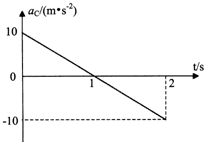
mCg=(mA+mB+mC)a1,
代入数据解得:${a}_{1}=2.5m/{s}^{2}$,
对A,根据牛顿第二定律:f=mAa1=2×2.5N=5N,
AB间最大静摩擦力:fm=μmBg=6.0N,
由于f<fm,假设成立,A与B相对静止.
(2)设ABC一起运动,以ABC为系统,根据牛顿第二定律有:
mC′g=(mA+mB+mC′)a2,
代入数据解得:${a}_{2}=5.0m/{s}^{2}$,
对A,根据牛顿第二定律得:f′=mAa2=2×5N=10N,
由于f′>fm,假设不成立,A与B相对滑动.
对A,根据牛顿第二定律,μmBg=mAaA,代入数据解得:${a}_{A}=3.0m/{s}^{2}$,
对BC为系统,根据牛顿第二定律:
mC′g-μmBg=(mB+mC′)aB,
代入数据解得:${a}_{B}=6.0m/{s}^{2}$.
设经t1时间B运动到A的右端,则有:$\frac{1}{2}{a}_{B}{{t}_{1}}^{2}-\frac{1}{2}{a}_{A}{{t}_{1}}^{2}=L$,
代入数据解得:t1=1.0s.
B第一段的位移:${s}_{1}=\frac{1}{2}{a}_{B}{{t}_{1}}^{2}=\frac{1}{2}×6×1m=3m$.
经t1时间B运动的速度:v1=aBt1=6×1m/s=6m/s,
B在光滑平面上滑动,对BC为系统,根据牛顿第二定律:
mC′g=(mB+mC′)aB′,
代入数据解得:${a}_{B}′=7.5m/{s}^{2}$,
B第二段的位移为:${s}_{2}={v}_{1}(t-{t}_{1})+\frac{1}{2}{a}_{B}(t-{t}_{1})^{2}$,
代入数据解得:s2=9.75m,
物块C下降的高度:h=s1+s2=3+9.75m=12.75m.
(3)设C与竖直面的动摩擦因数为μ′,
令k=20N/s,
根据图乙可得,F=kt,
对C水平方向:N=F,
C受摩擦力fC=μ′N,
以C为对象,有:mCg-fC=mCaC,
联立解得:${a}_{C}=g-\frac{μ′kt}{{m}_{C}}=(10-20μ′t)m/{s}^{2}$,
由上式可得如图的图象,t=t′=2s,物块v=0,则:${a}_{C}=-10m/{s}^{2}$,
代入数据解得:μ′=0.5.
由图可知t=1s时速度最大,最大速度等于图线与坐标轴围成的面积,有:${v}_{m}=\frac{1}{2}×1×10m/s=5m/s$.
答:(1)A与B相对静止.
(2)物块C下降的高度为12.75m.
(3)物块C与竖直面之间的动摩擦因数为0.5,此过程中的最大速度为5m/s.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,涉及多过程问题,难度较大,综合性较强,关键理清物体的运动规律,结合牛顿第二定律和运动学公式进行求解.对于第三问,得出C的加速度表达式是关键,知道a-t图线围成的面积表示速度的变化量.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中物理 来源: 题型:多选题
| A. | mgH-$\frac{1}{2}$mv2 | B. | (mgsinθ-ma)s | C. | μmgs cosθ | D. | mgH |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
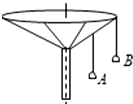 如图所示,“旋转秋千”中的两个座椅A、B质量相等,通过相同长度的缆绳悬挂在旋转圆盘上.不考虑空气阻力的影响,当旋转圆盘绕竖直的中心轴匀速转动时,下列说法正确的是( )
如图所示,“旋转秋千”中的两个座椅A、B质量相等,通过相同长度的缆绳悬挂在旋转圆盘上.不考虑空气阻力的影响,当旋转圆盘绕竖直的中心轴匀速转动时,下列说法正确的是( )| A. | A与B的角速度大小相等 | |
| B. | A与B的向心加速度大小相等 | |
| C. | 悬挂A的缆绳所受的拉力比悬挂B的小 | |
| D. | 悬挂A、B的缆绳与竖直方向的夹角相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图,半径为R的四分之一的光滑圆弧轨道,轨道下端与水平面相切,一质量为m的物体从顶端由静止沿轨道下滑,g=10m/s2 ,求在最低点时轨道受到的压力F.
如图,半径为R的四分之一的光滑圆弧轨道,轨道下端与水平面相切,一质量为m的物体从顶端由静止沿轨道下滑,g=10m/s2 ,求在最低点时轨道受到的压力F.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
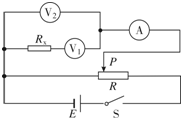 用如图所示的电路可同时测量定值电阻和电压表最小量程的内电阻.图中V1、V2为两块相同规格的多量程待测电压表,Rx为较大阻值的待测定值电阻,A为电流表,R为滑动变阻器,E为电源,S为电键.
用如图所示的电路可同时测量定值电阻和电压表最小量程的内电阻.图中V1、V2为两块相同规格的多量程待测电压表,Rx为较大阻值的待测定值电阻,A为电流表,R为滑动变阻器,E为电源,S为电键.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | B<0.2T | B. | B=0.2T | C. | B<5T | D. | B≥5T |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
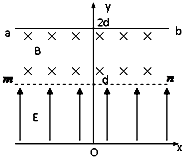 如图所示,在xoy坐标系坐标原点O处有甲、乙二粒子,其中甲沿x轴正方向发射,乙粒子沿y轴的正方向,它们的速度大小均为v0,在0<y<d的区域内分布有指向y轴正方向的匀强电场,场强大小为E=$\frac{3m{{v}_{0}}^{2}}{2qd}$,其中q与m分别二粒子的电量和质量;在d<y<2d的区域内分布有垂直于xoy平面向里的匀强磁场,mn为电场和磁场的边界.ab为一块很大的平面感光板垂直于xoy平面且平行于x轴,放置于y=2d处,如图所示.(q、d、m、v0均为已知量,不考虑粒子的重力及粒子间的相互作用),求:
如图所示,在xoy坐标系坐标原点O处有甲、乙二粒子,其中甲沿x轴正方向发射,乙粒子沿y轴的正方向,它们的速度大小均为v0,在0<y<d的区域内分布有指向y轴正方向的匀强电场,场强大小为E=$\frac{3m{{v}_{0}}^{2}}{2qd}$,其中q与m分别二粒子的电量和质量;在d<y<2d的区域内分布有垂直于xoy平面向里的匀强磁场,mn为电场和磁场的边界.ab为一块很大的平面感光板垂直于xoy平面且平行于x轴,放置于y=2d处,如图所示.(q、d、m、v0均为已知量,不考虑粒子的重力及粒子间的相互作用),求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com