
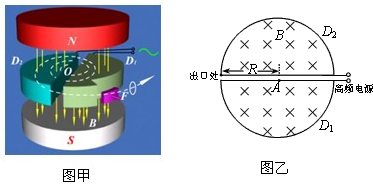
分析 (1)根据动能定理求出粒子第一次加速后进入磁场的速度,然后根据洛伦兹力提供向心力,列式求出质子在磁场中的轨道半径.
(2)设质子从静止开始加速到出口处运动了n圈,质子在出口处的速度为v.根据动能定理、牛顿第二定律和周期和时间关系结合求解.
(3)求出rk所对应的加速次数和rk+1所对应的加速次数即可求出它们所对应的轨道半径,然后作差即可求出rk和rk+1,从而求出△rk,运用同样的方法求出△rk+1,比较△rk和△rk+1即可得出答案.
解答 解:(1)设质子第1次经过狭缝被加速后的速度为v1
由动能定理得 $qU=\frac{1}{2}mv_1^2$…①
由牛顿第二定律有 $q{v_1}B=m\frac{v_1^2}{r_1}$…②
联立①②解得:${r_1}=\frac{1}{B}\sqrt{\frac{2mU}{q}}$
(2)设质子从静止开始加速到出口处运动了n圈,质子在出口处的速度为v,则
$2nqU=\frac{1}{2}m{v^2}$…③
$qvB=m\frac{v^2}{R}$…④
质子圆周运动的周期 $T=\frac{2πm}{qB}$…⑤
质子运动的总时间 t=nT…⑥
联立③④⑤⑥解得 $R=\sqrt{\frac{2Ut}{πB}}$
(3)(方法1)设k为同一盒子中质子运动轨道半径的序数,相邻的轨道半径分别为rk,rk+1(rk<rk+1),△rk=rk+1-rk,在相应轨道上质子对应的速度大小分别为vk,vk+1,D1、D2之间的电压为U,由动能定理知$2qU=\frac{1}{2}mv_{k+1}^2-\frac{1}{2}mv_k^2$…⑦
由洛伦兹力充当质子做圆周运动的向心力,知${r_k}=\frac{{m{v_k}}}{qB}$,则$2qU=\frac{{{q^2}{B^2}}}{2m}(r_{k+1}^2-r_k^2)$⑧
整理得 $△{r_k}=\frac{4mU}{{q{B^2}({r_{k+1}}+{r_k})}}$…⑨
相邻轨道半径rk+1,rk+2之差△rk+1=rk+2-rk+1
同理 $△{r_{k+1}}=\frac{4mU}{{q{B^2}({r_{k+2}}+{r_{k+1}})}}$
因U、q、m、B均为定值,且因为rk+2>rk,比较△rk与△rk+1得△rk+1<△rk.
(方法2)设k为同一盒子中质子运动轨道半径的序数,相邻的轨道半径分别为rk-1、rk、rk+1,(rk-1<rk<rk+1).
由$2kqU=\frac{1}{2}m{v_k}^2$ 及 $q{v_k}B=m\frac{v_k^2}{r_k}$ 得 ${r_k}=\frac{2}{B}\sqrt{\frac{mU}{q}}\sqrt{k}$
得$△{r_k}_{-1}={r_k}-{r_{k-1}}=\frac{2}{B}\sqrt{\frac{mU}{q}}(\sqrt{k}-\sqrt{k-1})$$△{r_k}={r_{k+1}}-{r_k}=\frac{2}{B}\sqrt{\frac{mU}{q}}(\sqrt{k+1}-\sqrt{k})$
假设$(\sqrt{k}-\sqrt{k-1})$>$(\sqrt{k+1}-\sqrt{k})$有$2\sqrt{k}>\sqrt{k+1}+\sqrt{k-1}$
两边平方得$k>\sqrt{{k^2}-1}$结果正确,说明假设成立.
所以△rk-1>△rk.
答:(1)质子第1次经过狭缝被加速后进入D形盒运动轨道的半径r1是$\frac{1}{B}\sqrt{\frac{2mU}{q}}$.
(2)D形盒半径为R是$\sqrt{\frac{2Ut}{πB}}$.
(3)随轨道半径r的增大,同一盒中相邻轨道的半径之差△r减小.
点评 本题的难点是(3),要求△rk需要知道rk和rk+1,同理算出△rk+1,对△rk和△rk+1,即可得出答案.


科目:高中物理 来源: 题型:多选题
 如图,AB为竖直面内半圆的水平直径.从A点水平抛出两个小球,小球l的抛出速度为v1、小2的抛出速度为v2.小球1落在C点、小球2落在D点,C,D两点距水平直径分别为圆半径的0.8倍和l倍.小球l的飞行时间为t1,小球2的飞行时间为t2.则( )
如图,AB为竖直面内半圆的水平直径.从A点水平抛出两个小球,小球l的抛出速度为v1、小2的抛出速度为v2.小球1落在C点、小球2落在D点,C,D两点距水平直径分别为圆半径的0.8倍和l倍.小球l的飞行时间为t1,小球2的飞行时间为t2.则( )| A. | t1=t2 | B. | t1<t2 | C. | v1:v2=4:$\sqrt{5}$ | D. | v1:v2=3:$\sqrt{5}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 子弹射出枪口时的速度为800m/s | |
| B. | 小球在空中做竖直上抛运动,2s末的速度为3m/s | |
| C. | 某高速公路限速标志上的限速为90km/h | |
| D. | 汽车从永州站行驶到长沙站,全程的速度为80km/h |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
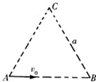 如图所示,比荷为$\frac{e}{m}$的电子以速度v0沿AB边射入边长为a的等边三角形的匀强磁场区域中.为使电子从BC边穿出磁场,磁感应强度B的取值范围为( )
如图所示,比荷为$\frac{e}{m}$的电子以速度v0沿AB边射入边长为a的等边三角形的匀强磁场区域中.为使电子从BC边穿出磁场,磁感应强度B的取值范围为( )| A. | B=$\frac{\sqrt{3}m{v}_{0}}{ae}$ | B. | B<$\frac{\sqrt{3}m{v}_{0}}{ae}$ | C. | B=$\frac{2m{v}_{0}}{ae}$ | D. | B<$\frac{2m{v}_{0}}{ae}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,理想变压器的原线圈两端接u=220$\sqrt{2}$sin100πt(V)的交流电源上副线圈两端接R=55Ω的负载电阻,原、副线圈匝数之比为2:1,电流表、电压表均为理想电表.下列说法正确的是( )
如图所示,理想变压器的原线圈两端接u=220$\sqrt{2}$sin100πt(V)的交流电源上副线圈两端接R=55Ω的负载电阻,原、副线圈匝数之比为2:1,电流表、电压表均为理想电表.下列说法正确的是( )| A. | 原线圈中的输入功率为220$\sqrt{2}$W | |
| B. | 原线圈中电流表的读数为1 A | |
| C. | 副线圈中电压表的读数为110$\sqrt{2}$V | |
| D. | 副线圈中输出交流电的周期为0.01s |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 点电荷为理想模型,实际并不存在 | |
| B. | 体积很大的带电体一定不能看作点电荷 | |
| C. | 只有体积很小的带电体,才能看作点电荷 | |
| D. | 点电荷一定是电荷量很小的带电体 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示的装置中,斜面光滑,倾角a=37°,质量为10kg的小球放置在斜面上,当装置以4m/s2的加速度竖直上升时,求:
如图所示的装置中,斜面光滑,倾角a=37°,质量为10kg的小球放置在斜面上,当装置以4m/s2的加速度竖直上升时,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
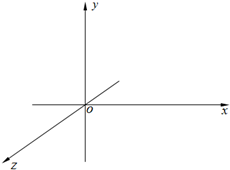 如图Ox、Oy、Oz为相互垂直的坐标轴,Oy轴为竖直方向,整个空间存在竖直向下的匀强磁场,磁感应强度大小为B.现有一质量为m、电量为q的小球从坐标原点O以速度v0沿Ox轴正方向抛出(不计空气阻力,重力加速度为g).求:
如图Ox、Oy、Oz为相互垂直的坐标轴,Oy轴为竖直方向,整个空间存在竖直向下的匀强磁场,磁感应强度大小为B.现有一质量为m、电量为q的小球从坐标原点O以速度v0沿Ox轴正方向抛出(不计空气阻力,重力加速度为g).求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com