

分析 (1)在0-kT时间内,根据动能定理求出电子穿出B板后的速度,在偏转电场中,电子做类平抛运动,根据牛顿第二定律和运动学公式得到偏转距离.根据推论:电子射出偏转电场后,好像从“中点射出”,得到打在荧光屏上的坐标.再运用同样的方法求出在kT-T 时间内,电子打在荧光屏上的坐标,即可求得这两个发光点之间的距离.
(2)要求在某一时刻形成均匀分布的一段电子束,前后两段电子束的长度必须相等,分别得到电子束长度的表达式,根据相等关系即可求得k.
解答 解:(1)电子经过电容器内的电场后,速度要发生变化.
在0-kT时间内,设穿出B板后速度变为v1,由动能定理得:
-eU0=$\frac{1}{2}$mv12-$\frac{1}{2}$mv02,
将U0=$\frac{m{{v}_{0}}^{2}}{6e}$,代入后解得:v1=$\sqrt{\frac{4e{U}_{0}}{m}}$.
在偏转电场中,电子运动时间t1=$\frac{L}{{v}_{1}}$,
侧移量y1=$\frac{1}{2}$at12=$\frac{e{U}_{0}{L}^{2}}{2md{{v}_{1}}^{2}}$,
解得:y1=$\frac{{L}^{2}}{8d}$.
根据偏转电场中的推论“似是中点来”其打在荧光屏上的坐标y1′=2y1=$\frac{{L}^{2}}{4d}$,
在kT-T 时间内,穿出B板后速度变为v2,同理可得,
eU0=$\frac{1}{2}$mv12-$\frac{1}{2}$mv02,
v2=$\sqrt{\frac{8e{U}_{0}}{m}}=\sqrt{2}{v}_{1}$,
y2=$\frac{{L}^{2}}{16d}$.
y2′=2y2=$\frac{{L}^{2}}{8d}$.
荧光屏上两个发光点之间的距离△y=y1′-y2′=$\frac{{L}^{2}}{8d}$.
(2)要求在某一时刻形成均匀分布的一段电子束,前后两段电子束的长度必须相等(且刚好重叠),第一束长度:l1=v1•kT,
第二束长度:l2=v2•(T-kT);
l1=l2
即v1•kT=$\sqrt{2}$ v1•(1-k)T,
解得k=$\frac{\sqrt{2}}{\sqrt{2}+1}$≈0.59.
答:(1)这两个发光点之间的距离为$\frac{{L}^{2}}{8d}$;
(2)k值为0.59.
点评 本题利用带电粒子在匀强电场中的类平抛运动及其相关知识列方程进行解答,关键要分析出临界条件和隐含的条件.


科目:高中物理 来源: 题型:实验题
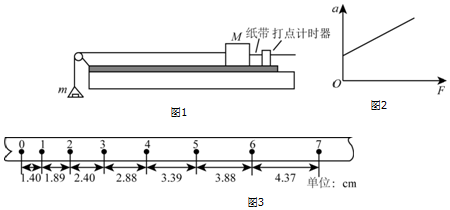
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
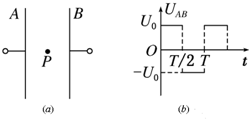
| A. | t=0由静止释放该粒子,一定能到达B板 | |
| B. | t=$\frac{T}{4}$由静止释放该粒子,可能到达B板 | |
| C. | 在0<t<$\frac{T}{2}$和$\frac{T}{2}$<t<T两个时间段内运动的粒子加速度相同 | |
| D. | 在$\frac{T}{4}$<t<$\frac{T}{2}$期间由静止释放该粒子,一定能到达A板 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
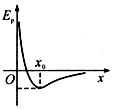 两个点电荷固定于x轴上,电量大小分别为Q和4Q,在它们形成的电场中,有一个带正电的试探电荷q从无限远处移向坐标原点O,其电势能EP随位置变化的关系如图所示曲线.当x→0时,电势能EP→∞;当x→∞时,电势能EP→0;电势能为最小值的位置坐标为x0.试根据图线提供的信息,确定在x轴的正半轴上各点场强方向为(0~x0)内沿x轴正方向,(x0~+∞)内沿x轴负方向;这两个点电荷在x轴上的位置是Q(0,0),-4Q(-x0,0)..
两个点电荷固定于x轴上,电量大小分别为Q和4Q,在它们形成的电场中,有一个带正电的试探电荷q从无限远处移向坐标原点O,其电势能EP随位置变化的关系如图所示曲线.当x→0时,电势能EP→∞;当x→∞时,电势能EP→0;电势能为最小值的位置坐标为x0.试根据图线提供的信息,确定在x轴的正半轴上各点场强方向为(0~x0)内沿x轴正方向,(x0~+∞)内沿x轴负方向;这两个点电荷在x轴上的位置是Q(0,0),-4Q(-x0,0)..查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | A车一定能追上B车,且A车由刹车到追上B车所用的时间为10s | |
| B. | A车一定能追上B车,且A车由刹车到追上B车所用的时间为20s | |
| C. | A车一定不能追上B车,且A、B两车的最近距离为100m | |
| D. | A车一定不能追上B车,且A、B两车的最近距离为50m |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 公式E=$\frac{F}{q}$只适用于真空中点电荷产生的电场 | |
| B. | 公式E=$\frac{F}{q}$中F是放入电场中的电荷所受的力,q是放入电场中的电荷的电量 | |
| C. | 在公式F=k$\frac{{{Q_1}{Q_2}}}{r^2}$,k$\frac{Q_2}{r^2}$是点电荷Q2产生的电场在点电荷Q1处的场强大小;而k$\frac{Q_1}{r^2}$是点电荷Q1产生的电场在点电荷Q2处的场强的大小 | |
| D. | 电场强度E与电场力F成正比,与放入电荷的电量q成反比 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
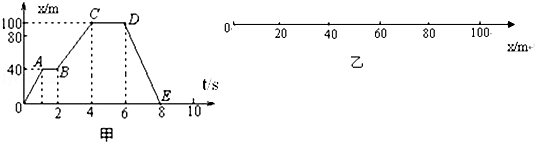
| A. | 根据图象A、B点在图乙所示的位置坐标轴上的位置为40m、60m处 | |
| B. | 求出前4s内的平均速度为20m/s | |
| C. | 第5s末的瞬时速度0m/s | |
| D. | 求出第7s末的瞬时速度50m/s |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com