Question

在香港海洋公园的游乐场中，有一台大型游乐机叫“跳楼机”.参加游乐的游客被安全带固定在座椅上，由电动机将座椅提升到40m高处，座椅沿光滑杆自由下落一段高度后开始受到压缩空气提供的恒定阻力，下落36m后速度刚好减小到零.这一过程经历的总时间是6s.求座椅被释放后，自由下落的高度有多高；在减速阶段，座椅对游客的弹力是游客体重的多少倍.

Answer 1

【解析】  座椅释放后自由下落的高度为
h′=H-h=40m-36m=4m
座椅下落高度h′时的速度是
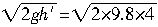
v′=m/s=8.85m/s
座椅下落高度h′时的时间是
t′=
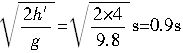
减速阶段，座椅的加速度大小是
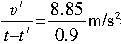
a==1.71m/s²
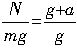
设游客的质量为m，座椅对游客的支持力为N，由牛顿第二定律得N-mg=ma，即N=m（g+a）.则座椅对游客的支持力与游客的重力的比值是n==1.2.
【试题分析】