
 如图所示,倾角为θ的固定粗糙斜面上有一物块A,物块到斜面底端的高度为h,紧靠斜面底端有一长为L的长木板B停放在光滑的水平面上,斜面底端刚好与长木板上表面左端接触,长木板上表面粗糙,右端与-$\frac{1}{4}$圆弧面C粘接在一起,圆弧面左端与木板平滑相接,现释放物块A让其从斜面上滑下.圆弧面表面光滑,圆弧面的半径为R,物块与斜面长木板表面的动摩擦因数均为μ,A、B、C三者的质量相等,重力加速度大小为g,不计物块A从斜面滑上木板时的机械能损失.
如图所示,倾角为θ的固定粗糙斜面上有一物块A,物块到斜面底端的高度为h,紧靠斜面底端有一长为L的长木板B停放在光滑的水平面上,斜面底端刚好与长木板上表面左端接触,长木板上表面粗糙,右端与-$\frac{1}{4}$圆弧面C粘接在一起,圆弧面左端与木板平滑相接,现释放物块A让其从斜面上滑下.圆弧面表面光滑,圆弧面的半径为R,物块与斜面长木板表面的动摩擦因数均为μ,A、B、C三者的质量相等,重力加速度大小为g,不计物块A从斜面滑上木板时的机械能损失.分析 (1)由动能定理求物块A到达斜面底端时的速度大小v;
(2)先由动能定理求出物块A到达斜面底端时的速度表达式.物块A恰好能滑到圆弧面C的最高点时,A与C的速度相同.由A、B、C系统的水平动量守恒和能量守恒结合求高度h1.
(3)最终物块A停留在长木板B上,由水平动量守恒列式,求出最终三者的共同速度.再由能量守恒列式求s.
解答 解:(1)物块A在斜面上下滑的过程,由动能定理得:
mgh-μmgcosθ•$\frac{h}{sinθ}$=$\frac{1}{2}m{v}^{2}$
解得:v=$\sqrt{2gh-\frac{2μgh}{tanθ}}$
(2)当物块开始下滑时到斜面底端的高度h1时,物块A在斜面上下滑的过程,由动能定理得:
mgh1-μmgcosθ•$\frac{{h}_{1}}{sinθ}$=$\frac{1}{2}m{v}_{1}^{2}$
解得:v1=$\sqrt{2g{h}_{1}-\frac{2μg{h}_{1}}{tanθ}}$
设物块A滑到圆弧面C的最高点时的速度大小为v2,取向右为正方向,由水平动量守恒得:
mv1=3mv2.
由功能关系有:μmgL=$\frac{1}{2}m{v}_{1}^{2}$-$\frac{1}{2}$×3mv22-mgR
解得:h1=$\frac{3(μL+R)tanθ}{2(tanθ-μ)}$
(3)经分析可知,当物块A最终停留在长木板B上时,物块、木板和圆弧面具有共同的速度,设为v3.根据动量守恒定律得:
mv1=3mv3.
上式中 v1=$\sqrt{2g{h}_{1}-\frac{2μg{h}_{1}}{tanθ}}$,且 h1=$\frac{3(μL+R)tanθ}{2(tanθ-μ)}$
由功能关系有:μmg(L+s)=$\frac{1}{2}m{v}_{1}^{2}$-$\frac{1}{2}•3m{v}_{3}^{2}$
解得:s=$\frac{R}{μ}$
答:(1)物块A到达斜面底端时的速度大小v是$\sqrt{2gh-\frac{2μgh}{tanθ}}$;
(2)改变物块A由静止释放的位置,若物块A恰好能滑到圆弧面C的最高点,其开始下滑时到斜面底端的高度h1是$\frac{3(μL+R)tanθ}{2(tanθ-μ)}$.
(3)物块A从圆弧面最高点返回后停留在长木板B上的位置到长木板右端的距离s是$\frac{R}{μ}$.
点评 解决本题的关键是要把握功与能的关系,挖掘隐含的临界条件:物块到达C的最高点时三个物体的速度相等.最终物块A停留在B上时三者速度又相同.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中物理 来源: 题型:选择题

| A. | t=0.01s时刻穿过线框回路的磁通量为零 | |
| B. | 交流发电机的转速为100r/s | |
| C. | 灯泡的额定电压为220$\sqrt{2}$V | |
| D. | 变压器原线圈中电流表示数为2A |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,一固定的足够长的竖直气缸有一大一小两个同轴圆筒组成,两圆筒中各有一个活塞,已知大活塞的质量为m1=1.50kg,横截面积为s1=80.0cm2,小活塞的质量为m2=2.50kg,横截面积为s2=40.0cm2,两活塞用刚性轻杆连接,活塞的厚度可以忽略,间距保持为l=40.0cm,气缸外大气压强为p=1.00×105Pa.初始时大活塞与小圆筒底部相距$\frac{l}{2}$,两活塞间封闭气体的温度为T1=495K,现气缸内气体温度缓慢改变,活塞缓慢移动,忽略两活塞与气缸壁之间的摩擦,重力加速度g取10m/s2.求:
如图所示,一固定的足够长的竖直气缸有一大一小两个同轴圆筒组成,两圆筒中各有一个活塞,已知大活塞的质量为m1=1.50kg,横截面积为s1=80.0cm2,小活塞的质量为m2=2.50kg,横截面积为s2=40.0cm2,两活塞用刚性轻杆连接,活塞的厚度可以忽略,间距保持为l=40.0cm,气缸外大气压强为p=1.00×105Pa.初始时大活塞与小圆筒底部相距$\frac{l}{2}$,两活塞间封闭气体的温度为T1=495K,现气缸内气体温度缓慢改变,活塞缓慢移动,忽略两活塞与气缸壁之间的摩擦,重力加速度g取10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | 电源正极应接在P点,光电子从电极K发出 | |
| B. | 电源正极应接在Q点,光电子从电极K发出 | |
| C. | 电源正极应接在P点,光电子从电极A发出 | |
| D. | 电源正极应接在Q点,光电子从电极A发出 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
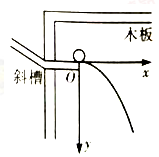 在“研究平抛物体的运动”的实验中:
在“研究平抛物体的运动”的实验中:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 如图所示,吊篮A、物块B和物块C三者的质量均为m,物块B、C之间用轻弹簧连接,重力加速度为g,将悬挂吊篮的轻绳烧断的瞬间,吊篮A的加速度大小为1.5g,物块B对吊篮A底部的压力大小为0.5mg.
如图所示,吊篮A、物块B和物块C三者的质量均为m,物块B、C之间用轻弹簧连接,重力加速度为g,将悬挂吊篮的轻绳烧断的瞬间,吊篮A的加速度大小为1.5g,物块B对吊篮A底部的压力大小为0.5mg.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 做曲线运动的物体,其速度大小一定变化 | |
| B. | 做曲线运动的物体,其加速度大小一定变化 | |
| C. | 在平衡力作用下,物体可以做曲线运动 | |
| D. | 在合力大小不变的情况下,物体可能做曲线运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
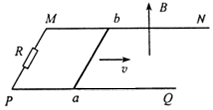 如图所示,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P之间接有阻值为R的定值电阻.导体棒ab长l=0.5m,其电阻为r,与导轨接触良好.整个装置处于方向竖直向上的匀强磁场中,磁感应强度B=0.4T.现使ab以v=10m/s的速度向右做匀速运动.
如图所示,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P之间接有阻值为R的定值电阻.导体棒ab长l=0.5m,其电阻为r,与导轨接触良好.整个装置处于方向竖直向上的匀强磁场中,磁感应强度B=0.4T.现使ab以v=10m/s的速度向右做匀速运动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com