
| 弹簧压缩量x/cm | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 |
| 小球飞行水平距离s/cm | 20.10 | 30.00 | 40.10 | 49.90 | 69.90 |

分析 (1)根据平抛运动的规律求出平抛运动的初速度,根据能量守恒求出释放小球前弹簧的弹性势能.
(2)由表中数据可看出,在误差范围内,s正比于x,从而得出表格中缺少的数据.
(3)先从实验数据得出弹簧的压缩量与小球的射程的关系,再结合第一小问中结论得到弹性势能与小球的射程的关系,最后综合出弹簧的弹性势能EP与弹簧长度的压缩量x之间的关系
解答 解:(1)由平抛运动规律有:s=vt,
h=$\frac{1}{2}$gt2,
得:v=s$\sqrt{\frac{g}{2h}}$.
由机械能守恒定律得:EP=$\frac{1}{2}$mv2=$\frac{mg{s}^{2}}{4h}$
释放小球前弹簧的弹性势能表达式为Ep=$\frac{mg{s}^{2}}{4h}$;
(2)由表中数据可看出,在误差范围内,s正比于x,s=20x,则当弹簧压缩量x=3.00cm时,s=60.00cm
(3)由平抛运动规律有L=vt,y=$\frac{1}{2}$gt2,
得v=L $\sqrt{\frac{g}{2y}}$根据Ep=$\frac{mg{s}^{2}}{4h}$,
所以弹簧弹性势能与弹簧压缩量x之间得关系式应为:Ep=$\frac{100mg{x}^{2}}{h}$
根据能量守恒,则有:$\frac{1}{2}$mv2=$\frac{100mg{x}^{2}}{h}$
联立上式,解得弹簧得压缩量应该为:x=$\frac{L}{20}\sqrt{\frac{h}{y}}$.
故答案为:(1)$\frac{mg{s}^{2}}{4h}$;(2)60.00;(3)$\frac{L}{20}\sqrt{\frac{h}{y}}$
点评 该题首先是考察了平抛运动的应用,解决关于平抛运动的问题常用的方法是沿着水平和竖直两个方向进行分解,运用各方向上的运动规律进行解答.利用x与s之间的关系求出弹簧弹性势能与弹簧压缩量x之间的关系式.考察了在现有知识的基础上对实验改装后的情况进行分析求解,考察了同学们的应变能力.还考察了对实验误差的分析,让学生学会试验中某个量发生变化导致结果如何变化的分析


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 地球半径和地球的自转周期 | B. | 月球绕地球的公转周期 | ||
| C. | 地球的平均密度和太阳的半径 | D. | 地球半径和地球表面的重力加速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
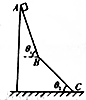 如图所示,AB与BC是两个场地相同的斜面,但倾角不同,AB与水平方向夹角为θ1,BC与水平方向夹角为θ2,两斜面间用光滑的小圆弧连接,物体通过时无能量损失,一物块从A点由静止释放,运动到C点速度刚好为0.已知物块与两斜面的动摩擦因数相同,则物块与两斜面的动摩擦因数为( )
如图所示,AB与BC是两个场地相同的斜面,但倾角不同,AB与水平方向夹角为θ1,BC与水平方向夹角为θ2,两斜面间用光滑的小圆弧连接,物体通过时无能量损失,一物块从A点由静止释放,运动到C点速度刚好为0.已知物块与两斜面的动摩擦因数相同,则物块与两斜面的动摩擦因数为( )| A. | $\frac{2}{cos{θ}_{1}+cot{θ}_{2}}$ | B. | $\frac{cos{θ}_{1}+cos{θ}_{2}}{sin{θ}_{1}+sin{θ}_{2}}$ | ||
| C. | $\frac{sin{θ}_{1}-sin{θ}_{2}}{cos{θ}_{1}-cos{θ}_{2}}$ | D. | $\frac{sin{θ}_{1}+sin{θ}_{2}}{cos{θ}_{1}+cos{θ}_{2}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 垂直纸面匀强磁场O点静止放着一个放射性原子核,它发生衰变后粒子和反冲核轨迹如图所示,由图可以判断( )
垂直纸面匀强磁场O点静止放着一个放射性原子核,它发生衰变后粒子和反冲核轨迹如图所示,由图可以判断( )| A. | 这是α衰变 | B. | 这是β衰变 | ||
| C. | 轨迹a是顺时针方向 | D. | 轨迹b是顺时针方向 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 质点在离该星球中心r处时受到的引力是G$\frac{Mm}{{r}^{2}}$ | |
| B. | 质点在离该星球中心r处时加速度是$\frac{GMr}{{R}^{3}}$ | |
| C. | 质点从隧道一端到星球中心运动时间小于到另一端的时间 | |
| D. | 历点先傲匀加速运动然后做匀减速运动 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com