
分析 (1)设乘客经过t时间与客车车头的位移为s0,通过位移关系求出运动的时间,时间有两个值,在这两个时间之间,乘客与客车车头的位移小于s0,则两个时间之差要保证大于等于t0,根据该关系求出乘客速度的最小值.
(2)
解答 解:(1)从客车由静止开始运动计时,经过时间t,客车前进的位移为:${s}_{1}=\frac{1}{2}a{t}^{2}$,
乘客前进的位移为:s2=vt
由题意有:s1+s-s2=s0
△t=t2-t1≥t0
得:$\frac{1}{2}a{t}^{2}+s-vt-{s}_{0}$=0,
即t=$\frac{v±\sqrt{{v}^{2}-2a(s-{s}_{0})}}{a}$,
所以有:△t=t2-t1=$\frac{v+\sqrt{{v}^{2}-2a(s-{s}_{0})}}{a}-\frac{v-\sqrt{{v}^{2}-2a(s-{s}_{0})}}{a}$=$\frac{2\sqrt{{v}^{2}-2a(s-{s}_{0})}}{a}$≥t0,
得v$≥\sqrt{2a(s-{s}_{0})+\frac{(a{t}_{0})^{2}}{4}}$
代入数据求得:v≥5m/s.
(2)在司机恰好能停车的情况下,追赶客车的过程中开始时人的速度大于车的速度,然后车的速度大于人的速度,所以当车与人的速度相等时,人与车之间的距离最小.则:v=at
所以:t=$\frac{v}{a}=\frac{5}{1}s=5$s
该过程中人的位移:x1=vt=5×5=25m
车的位移:${x}_{2}=\frac{1}{2}a{t}^{2}=\frac{1}{2}×1×{5}^{2}=12.5$m
人与车之间的距离:L′=S+x2-x1=32+12.5-25=19.5m
答:(1)该乘客追赶公交车的最小速度应为5m/s;
(2)经过5s时间乘客距离客车最近,最近距离是19.5m.
点评 该题属于运动学中的较难题,关键抓住乘客经过时间t与客车车头的位移为s0,还要注意乘客与客车车头位移在s0之内的时间差大于等于t0.


 53随堂测系列答案
53随堂测系列答案科目:高中物理 来源: 题型:实验题
 某研究性学习小组欲探究光滑斜面上物体下滑的加速度与物体质量及斜面倾角是否有关系.实验室提供如下器材:
某研究性学习小组欲探究光滑斜面上物体下滑的加速度与物体质量及斜面倾角是否有关系.实验室提供如下器材:| 质量 时间 t次数 | M | M+m | M+2m |
| 1 | 1.42 | 1.41 | 1.42 |
| 2 | 1.40 | 1.42 | 1.39 |
| 3 | 1.41 | 1.38 | 1.42 |
| L(m) | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| h(m) | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 |
| sinα=$\frac{h}{L}$ | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 |
| a(m/s2) | 0.97 | 1.950 | 2.925 | 3.910 | 4.900 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
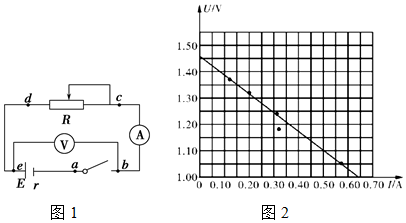
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
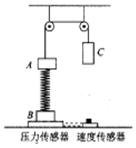 某同学利用图示装置来研究机械能守恒问题,设计了如下实验.
某同学利用图示装置来研究机械能守恒问题,设计了如下实验.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
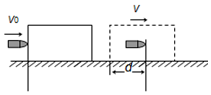 设质量为m的子弹以初速度v0射向静止在光滑水平面上的质量为M的木块,并留在木块中不再射出,子弹钻入木块深度为d.
设质量为m的子弹以初速度v0射向静止在光滑水平面上的质量为M的木块,并留在木块中不再射出,子弹钻入木块深度为d.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,a、b、c是地球大气层外圆形轨道上运动的三颗卫星,a和b质量相等且小于c的质量,则( )
如图所示,a、b、c是地球大气层外圆形轨道上运动的三颗卫星,a和b质量相等且小于c的质量,则( )| A. | b所需向心力最小 | |
| B. | b、c的周期相同且大于a的周期 | |
| C. | b、c的向心加速度大小相等,且大于a的向心加速度 | |
| D. | b、c的线速度大小相等,且大于a的线速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
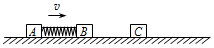 如图所示,质量均为m的两滑块A、B间压缩着一个弹性势能为mv2的轻弹簧,弹簧与A、B不栓接,滑块A、B用细线相连.A、B以相同的速度v沿光滑水平面匀速运动,能与质量也为m的静止滑块C发生正碰,且碰撞瞬间细线断裂,碰后B、C粘在一起.在以后的运动过程中.
如图所示,质量均为m的两滑块A、B间压缩着一个弹性势能为mv2的轻弹簧,弹簧与A、B不栓接,滑块A、B用细线相连.A、B以相同的速度v沿光滑水平面匀速运动,能与质量也为m的静止滑块C发生正碰,且碰撞瞬间细线断裂,碰后B、C粘在一起.在以后的运动过程中.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 同一时刻它们的加速度的大小一定相等 | |
| B. | 它们都做匀加速运动 | |
| C. | 静电力对它们都做正功 | |
| D. | 电势能减小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com