
如图所示,直线MN下方无磁场,上方空间存在两个匀强磁场,其分界线是半径为R的半圆,两侧的磁场方向相反且垂直于纸面,磁感应强度大小都为B,现有一质量为m、电荷量为q的带负电微粒从P点沿半径方向向左侧射出,最终打到Q点,不计微粒的重力。求:
(1)微粒在磁场中运动的周期;
(2)从P点到Q点,微粒的运动速度大小及运动时间;
(3)若向里磁场是有界的,分布在以O点为圆心、半径为R和2R的两半圆之间的区域,上述微粒仍从P点沿半径方向向左侧射出,且微粒仍能到达Q点,求其速度的最大值。

(1)![]()
(2)![]() (n=2,3,4……)。
(n=2,3,4……)。
![]() (n=2,4,6……);
(n=2,4,6……); (n=3,5,7……)
(n=3,5,7……)
(3)![]()
(1)由 ![]() (2分)
(2分)
![]() (2分)
(2分)
得![]() (1分)
(1分)
(2)粒子的运动轨迹将磁场边界分成n等分(n=2,3,4……)
由几何知识可得:![]() ;(2分)
;(2分)
![]() ; (2分)
; (2分)
又 ![]()
得 ![]() (n=2,3,4……) (2分)
(n=2,3,4……) (2分)
当n为偶数时,由对称性可得 ![]() (n=2,4,6……) (2分)
(n=2,4,6……) (2分)

当n为奇数时,t为周期的整数倍加上第一段的运动时间,即
 (n=3,5,7……) (2分)
(n=3,5,7……) (2分)
(3)由几何知识得![]() ;
;
![]() (2分)
(2分)
且不超出边界须有: ![]() (2分)
(2分)
得 ![]()
当n=2时 不成立,如图

比较当n=3、n=4时的运动半径,


知 当n=3时,运动半径最大,粒子的速度最大.
![]() (2分)
(2分)
得:![]() (1分)
(1分)


科目:高中物理 来源: 题型:
 如图所示,直线MN上方存在垂直纸面向里、磁感应强度大小为B的匀强磁场,现有一质量为m、带电荷量为+q的粒子在纸面内以某一速度从A点射入,其方向与MN成30°角,A点到MN的垂直距离为d,带电粒子重力不计.求:
如图所示,直线MN上方存在垂直纸面向里、磁感应强度大小为B的匀强磁场,现有一质量为m、带电荷量为+q的粒子在纸面内以某一速度从A点射入,其方向与MN成30°角,A点到MN的垂直距离为d,带电粒子重力不计.求:查看答案和解析>>
科目:高中物理 来源: 题型:
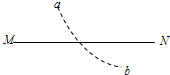 如图所示,直线MN是某电场中的一条电场线(方向未画出).虚线是一带电的粒子只在电场力的作用下,由a到b的运动轨迹,轨迹为一抛物线.下列判断正确的是( )
如图所示,直线MN是某电场中的一条电场线(方向未画出).虚线是一带电的粒子只在电场力的作用下,由a到b的运动轨迹,轨迹为一抛物线.下列判断正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:
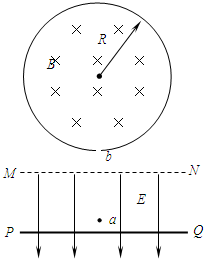 如图所示,直线MN的下方有竖直向下的匀强电场,场强大小为E=700V/m.在电场区域内有一个平行于MN的挡板PQ;MN的上方有一个半径为R=0.866m的圆形弹性围栏,在围栏区域内有图示方向的匀强磁场,磁感应强度大小为B=1.4T.围栏最低点一个小洞b,在b点正下方的电场区域内有一点a,a点到MN的距离d1=45cm,到PQ距离d2=5cm.现将一个质量为m=0.1g,带电量q=2×10-3C的带正电小球(重力不计),从a点由静止释放,在电场力作用下向下运动与挡板PQ相碰后电量减少到碰前的0.8倍,且碰撞前后瞬间小球的动能不变,不计小球运动过程中的空气阻力以及小球与围栏碰撞时的能量损失,试求:(已知1.2510=9.31,1.2511=11.628)
如图所示,直线MN的下方有竖直向下的匀强电场,场强大小为E=700V/m.在电场区域内有一个平行于MN的挡板PQ;MN的上方有一个半径为R=0.866m的圆形弹性围栏,在围栏区域内有图示方向的匀强磁场,磁感应强度大小为B=1.4T.围栏最低点一个小洞b,在b点正下方的电场区域内有一点a,a点到MN的距离d1=45cm,到PQ距离d2=5cm.现将一个质量为m=0.1g,带电量q=2×10-3C的带正电小球(重力不计),从a点由静止释放,在电场力作用下向下运动与挡板PQ相碰后电量减少到碰前的0.8倍,且碰撞前后瞬间小球的动能不变,不计小球运动过程中的空气阻力以及小球与围栏碰撞时的能量损失,试求:(已知1.2510=9.31,1.2511=11.628)查看答案和解析>>
科目:高中物理 来源: 题型:
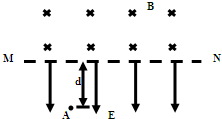 (2012?广东一模)如图所示,直线MN上方有匀强磁场,磁感应强度为B,方向垂直纸面向里;下方有方向向下的匀强电场,场强为E,一电子(电量e,质量为m)自A点由静止释放,A点到MN的距离为d.不计重力,求:
(2012?广东一模)如图所示,直线MN上方有匀强磁场,磁感应强度为B,方向垂直纸面向里;下方有方向向下的匀强电场,场强为E,一电子(电量e,质量为m)自A点由静止释放,A点到MN的距离为d.不计重力,求:查看答案和解析>>
科目:高中物理 来源: 题型:
如图所示,直线MN的下方有竖直向下的匀强电场,场强大小为E=700V/m。在电场区域内有一个平行于MN的挡板PQ;MN的上方有一个半径为R=0.866m的圆形弹性围栏,在围栏区域内有图示方向的匀强磁场,磁感应强度大小为B=1.4T。围栏最低点一个小洞b,在b点正下方的电场区域内有一点a,a点到MN的距离d1=45cm,到PQ距离d2=5cm。现将一个质量为m=0.1g ,带电量q=2×10-3C的带正电小球(重力不计),从a点由静止释放,在电场力作用下向下运动与挡板PQ相碰后电量减少到碰前的0.8倍,且碰撞前后瞬间小球的动能不变,不计小球运动过程中的空气阻力以及小球与围栏碰撞时的能量损失,试求:(已知![]() ,
,![]() )
)
⑴求出小球第一次与挡板PQ相碰后向上运动的距离;
⑵小球第一次从小洞b进入围栏时的速度大小;
⑶小球从第一次进入围栏到离开围栏经历的时间。
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com