
| A. | 向心加速度大小之比为9:1 | B. | 周期之比为1:27 | ||
| C. | 角速度大小之比为3:1 | D. | 轨道半径之比为1:3 |
分析 根据万有引力提供向心力,通过线速度的变化得出轨道半径的变化,从而得出向心力和周期及机械能的变化
解答 解:根据万有引力提供圆周运动向心力有$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{{v}_{\;}^{2}}{r}$,可得卫星的线速度$v=\sqrt{\frac{GM}{r}}$,可知当卫星线速度减小为原来的$\frac{1}{3}$,则半径增大为原来的9倍.
A、根据万有引力提供向心力有,$G\frac{Mm}{{r}_{\;}^{2}}=ma$,可知$a=\frac{GM}{{r}_{\;}^{2}}$,变轨前后轨道半径之比为1:9,向心加速度之比为81:1,故A错误;
B、根据万有引力提供向心力有,$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$,可知$T=\sqrt{\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{GM}}$,变轨前后轨道半径之比为1:9,周期之比为$\frac{{T}_{1}^{\;}}{{T}_{2}^{\;}}=\sqrt{\frac{{r}_{1}^{3}}{{r}_{2}^{3}}}=\sqrt{\frac{{1}_{\;}^{3}}{{9}_{\;}^{3}}}=\frac{1}{27}$,故B正确;
C、根据万有引力提供向心力有,$G\frac{Mm}{{r}_{\;}^{2}}=m{ω}_{\;}^{2}r$,可知$ω=\sqrt{\frac{GM}{{r}_{\;}^{3}}}$,变轨前后轨道半径之比为1:9,周期之比为$\frac{{ω}_{1}^{\;}}{{ω}_{2}^{\;}}=\sqrt{\frac{{r}_{2}^{3}}{{r}_{1}^{3}}}=\sqrt{\frac{{9}_{\;}^{3}}{{1}_{\;}^{3}}}=\frac{27}{1}$,故C错误;
D、由上述分析知变轨前后轨道半径之比为1:9,故D错误;
故选:B
点评 解决本题的关键掌握万有引力提供向心力,知道线速度、向心力、周期、机械能与轨道半径的关系


科目:高中物理 来源: 题型:选择题
| A. | 做平抛运动的物体 | B. | 被匀速吊起的集装箱 | ||
| C. | 跳伞运动员空中下降的过程 | D. | 随摩天轮做匀速圆周运动的小孩 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
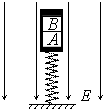 如图所示,质量均为m的A、B两物体叠放在劲度系数为k的竖直轻质弹簧上并保持静止,其中B带负电,电荷量大小为q,A始终不带电.现加上竖直向下的匀强电场,场强大小为$\frac{mg}{2q}$,当运动距离h时B与A分离.从开始运动到B和A刚分离的过程中,下列说法正确的是( )
如图所示,质量均为m的A、B两物体叠放在劲度系数为k的竖直轻质弹簧上并保持静止,其中B带负电,电荷量大小为q,A始终不带电.现加上竖直向下的匀强电场,场强大小为$\frac{mg}{2q}$,当运动距离h时B与A分离.从开始运动到B和A刚分离的过程中,下列说法正确的是( )| A. | B对A的压力一直减小 | B. | B物体的动能一直增加 | ||
| C. | 物体B机械能的增加量为$\frac{mgh}{2}$ | D. | 两物体运动的距离h=$\frac{3mg}{2k}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
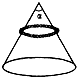 如图所示为固定在水平地面上的顶角为α的圆锥体,其表面光滑.有一质量为m、长为L的链条静止在圆锥体的表面上,已知重力加速度为g,若圆锥体对圆环的作用力大小为F,链条中的张力为T,则有( )
如图所示为固定在水平地面上的顶角为α的圆锥体,其表面光滑.有一质量为m、长为L的链条静止在圆锥体的表面上,已知重力加速度为g,若圆锥体对圆环的作用力大小为F,链条中的张力为T,则有( )| A. | F=mg | B. | F=$\frac{mg}{sin\frac{α}{2}}$ | C. | T=$\frac{mg}{πtan\frac{α}{2}}$ | D. | T=$\frac{mg}{2πtan\frac{α}{2}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 用如图所示的装置来验证动量守恒定律.图中PQ为斜槽,QR为水平槽.实验时先将a球从斜槽上某一固定位置G由静止开始滚下,落到位于水平地面的记录纸上,留下痕迹.关于小球落点的下列说法中正确的是( )
用如图所示的装置来验证动量守恒定律.图中PQ为斜槽,QR为水平槽.实验时先将a球从斜槽上某一固定位置G由静止开始滚下,落到位于水平地面的记录纸上,留下痕迹.关于小球落点的下列说法中正确的是( )| A. | 如果小球每一次都从同一点无初速释放,重复几次的落点落在同一位置 | |
| B. | 由于偶然因素存在,重复操作时小球的落点不重合是正常的,但落点应当比较密集 | |
| C. | 测定P点位置时,如果重复10次的落点分别为P1、P2、P3、…P10,则OP应取OP1、OP2、OP3…OP10的平均值,即OP=$\frac{1}{10}$(OP1+OP2+…+OP10的) | |
| D. | 用半径尽量小的圆把P1、P2、P3…P10圈住,这个圆的圆心就是入射球落点的平均位置P |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 液晶具有流动性,光学性质各向异性 | |
| B. | 气体扩散现象表明气体分子间存在斥力 | |
| C. | 热量总是自发的从分子平均动能大的物体传递到分子平均动能小的物体 | |
| D. | 机械能不可能全部转化为内能,内能也无法全部用来做功以转化成机械能 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 质量为m=1kg的物体,在竖直平面内高h=1m的光滑弧形轨道A点,以v0=4m/s的初速度沿轨道滑下,并进入BC轨道,最后停在C点,如图所示.(取g=10m/s2) 求:
质量为m=1kg的物体,在竖直平面内高h=1m的光滑弧形轨道A点,以v0=4m/s的初速度沿轨道滑下,并进入BC轨道,最后停在C点,如图所示.(取g=10m/s2) 求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,内壁光滑的导热气缸固定在水平地面上,用活塞把一定质量的理想气体封闭在气缸中.现用水平外力F作用于活塞杆,使活塞缓慢地向右移动,由状态①变化到状态②.如果环境保持恒温,则下图中可表示此过程的图象是( )
如图所示,内壁光滑的导热气缸固定在水平地面上,用活塞把一定质量的理想气体封闭在气缸中.现用水平外力F作用于活塞杆,使活塞缓慢地向右移动,由状态①变化到状态②.如果环境保持恒温,则下图中可表示此过程的图象是( )| A. | 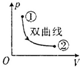 | B. |  | C. |  | D. | 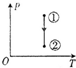 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com