
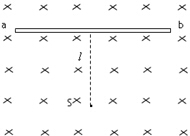
 ��ͼ��������ڴ�����ǿ�ų����ų�����ֱ��ֽ������Ÿ�Ӧǿ�ȵĴ�СB=0.60T���ų�����һ��ƽ��й��ab��������ų�����ƽ�У��ھ�ab�ľ���l=16cm������һ����״�Ħ�����ԴS�������������������ӣ������ӵ��ٶȶ���v=3.0��106m/s����֪�����ӵĵ��������֮��$\frac{q}{m}$=5.0��107C/kg����ֻ������ͼֽƽ�����˶��Ħ����ӣ���
��ͼ��������ڴ�����ǿ�ų����ų�����ֱ��ֽ������Ÿ�Ӧǿ�ȵĴ�СB=0.60T���ų�����һ��ƽ��й��ab��������ų�����ƽ�У��ھ�ab�ľ���l=16cm������һ����״�Ħ�����ԴS�������������������ӣ������ӵ��ٶȶ���v=3.0��106m/s����֪�����ӵĵ��������֮��$\frac{q}{m}$=5.0��107C/kg����ֻ������ͼֽƽ�����˶��Ħ����ӣ������� ��1���������ڴų���������Բ���˶��������������䵱��������������ӵİ뾶�����ϼ��ι�ϵ�����ab�ϱ����е�����ij��ȣ�
��2���˶�ʱ����켣��Բ�Ľdz����ȣ������ٽ�켣����Ϲ�ʽt=$\frac{��}{2��}T$��ʽ��⼴�ɣ�
���  �⣺��1�������Ӵ����磬���ڴų�������ʱ�뷽��������Բ���˶������������ṩ����������ţ�ٵڶ����ɵã�qvB=m$\frac{{v}^{2}}{r}$����
�⣺��1�������Ӵ����磬���ڴų�������ʱ�뷽��������Բ���˶������������ṩ����������ţ�ٵڶ����ɵã�qvB=m$\frac{{v}^{2}}{r}$����
�������ݽ�ã�r=0.1m=10cm��
�������ڴų�����Բ���˶������ڣ�T=$\frac{2��m}{qB}$=$\frac{2��}{5��1{0}^{7}��0.6}$=$\frac{2��}{3}$��10-7s��
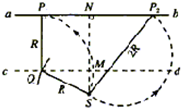
����2r��l��r����ͬ������Ħ����ӵ�Բ�켣����S���ɴ˿�֪��ijһԲ�켣��ͼ��N�����ab���У�����е�P���Ǧ������ܴ��е������Զ�㣻����P���λ�ã�����ƽ����ab��ֱ��cd��cd��ab�ľ���Ϊr����SΪԲ�ģ�rΪ�뾶��������cd��Q�㣬��Q��ab�Ĵ��ߣ�����ab�Ľ��㼴ΪP���ʣ�
NP1=$\sqrt{{r}^{2}-��l-r��^{2}}$����
�ٿ���N���Ҳ࣮�κΦ��������˶�����S�ľ��벻���ܳ���2R����2RΪ�뾶��SΪԲ����Բ����ab��N�Ҳ��P2�㣬�˼��Ҳ��ܴ���Զ�㣮
��ͼ�м��ι�ϵ�ã�NP2=$\sqrt{��2r��^{2}-{l}^{2}}$����
������P1P2=NP1+NP2����
������ֵ��P1P2=20cm��ab�ϱ������Ӵ��е�����ij��� P1P2=20cm��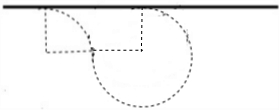 ��2����������Դ�Ƶ���ab�ľ���Ϊ10cm�������ӵĹ���뾶�����ڲ��䣻�����ٽ�켣����ͼ��ʾ��
��2����������Դ�Ƶ���ab�ľ���Ϊ10cm�������ӵĹ���뾶�����ڲ��䣻�����ٽ�켣����ͼ��ʾ��
���ʱ��Ϊ��tmax=$\frac{3}{4}T$
���ʱ��Ϊ��tmin=$\frac{1}{4}T$
�����Ӵ��ϵ����ʱ���Ϊ��
$��t={t}_{max}-{t}_{min}=\frac{T}{2}$=$\frac{��}{3}$��10-7s��
�𣺣�1��ab�Ϧ����Ӵ��е�����ij���Ϊ20cm��
��2����������Դ�Ƶ���ab�ľ���Ϊ10cm������ͬһʱ�̷�����Ĵ������Ӵ��ϵ����ʱ���Ϊ$\frac{��}{3}$��10-7s��
���� ���������ڴų��е��˶�����Ĺؼ�����ȷ��Բ�ĺͰ뾶�������ٽ�켣��Ȼ�����ɼ��ι�ϵ�������Ҫ������⣬����ؼ��ǻ����ٽ�켣�����ѣ�


 �߽�������ϵ�д�
�߽�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
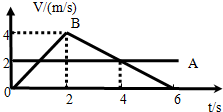 ��ͼ��ʾ��������A��Bͬʱ��һ�ص���ͬһ������ֱ���˶����ٶ�ͼ��������˵����ȷ���ǣ�������
��ͼ��ʾ��������A��Bͬʱ��һ�ص���ͬһ������ֱ���˶����ٶ�ͼ��������˵����ȷ���ǣ�������| A�� | ��4sʱ��A��B��ǰ�� | |
| B�� | ��������������ʱ���ǵ�2sĩ�͵�6sĩ | |
| C�� | �ڵ�2sĩ��B�˶��������ı� | |
| D�� | ��0sʱ��A���ٶ�Ϊ2m/s |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
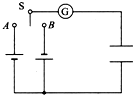 ��ͼ��ʾ����ԴA�ĵ�ѹΪ6V����ԴB�ĵ�ѹΪ8V���������ĵ���Ϊ200PF��������S����A���ȶ����ٺ���B���ٴδﵽ�ȶ����������������ͨ�������Ƶĵ����Ϊ��������
��ͼ��ʾ����ԴA�ĵ�ѹΪ6V����ԴB�ĵ�ѹΪ8V���������ĵ���Ϊ200PF��������S����A���ȶ����ٺ���B���ٴδﵽ�ȶ����������������ͨ�������Ƶĵ����Ϊ��������| A�� | 4��10-9C | B�� | 1.2��10-9C | C�� | 1.6��10-9C | D�� | 2.8��10-9C |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ţ�ٵ�һ������ʵ�鶨�� | |
| B�� | ţ�ٵ�һ����ֻ������˹��Եĸ��� | |
| C�� | ţ�ٵ�һ��������˵������ܵ��ĺ�����Ϊ��ʱ�����彫���ھ�ֹ״̬ | |
| D�� | ţ�ٵ�һ���ɼ���������岻����������ʱ���˶����ɣ�����������Ǹı������˶�״̬��ԭ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
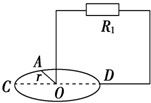 ��ͼ��ʾΪһԲ������װ�ã��õ���R=4���ĵ������ɰ뾶L=0.2m�ıպ�Բ����Բ��ΪO��COD��һ��ֱ������O��D����и��ص���R1=1��������Բ���о���B=0.5T����ǿ�ų���ֱ���洩��������r=1���ĵ����OA����Բ���������˶������ٶȦ�=300rad/s����OA����OC��ʱ��������
��ͼ��ʾΪһԲ������װ�ã��õ���R=4���ĵ������ɰ뾶L=0.2m�ıպ�Բ����Բ��ΪO��COD��һ��ֱ������O��D����и��ص���R1=1��������Բ���о���B=0.5T����ǿ�ų���ֱ���洩��������r=1���ĵ����OA����Բ���������˶������ٶȦ�=300rad/s����OA����OC��ʱ��������| A�� | Բ���ĵ繦��Ϊ1 W | B�� | Բ���ĵ繦��Ϊ2 W | ||
| C�� | ȫ��·�ĵ繦����С��Ϊ3 W | D�� | ȫ��·�ĵ繦�����Ϊ4.5 W |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
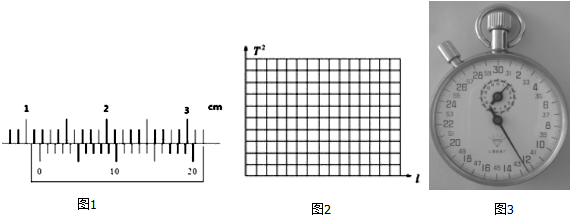
| l/m | 0.5 | 0.8 | 0.9 | 1.0 | 1.2 |
| T/s | 1.42 | 1.79 | 1.90 | 2.00 | 2.20 |
| T2/s2 | 2.02 | 3.20 | 3.61 | 4.00 | 4.84 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 5 | C�� | 7 | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
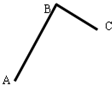 ��ͼ���������ȷֱ�ΪL1��L2�Ĺ⻬��AB��BC��B�㴹ֱ���ӣ�����ͼʾ��ʽ�̶�����ֱƽ����ʱ����һ������B���ɾ�ֹ�ͷţ��ֱ���BA��BC�����˵ĵ˾�����ʱ����ͬ�������ʱ��Ϊ��������
��ͼ���������ȷֱ�ΪL1��L2�Ĺ⻬��AB��BC��B�㴹ֱ���ӣ�����ͼʾ��ʽ�̶�����ֱƽ����ʱ����һ������B���ɾ�ֹ�ͷţ��ֱ���BA��BC�����˵ĵ˾�����ʱ����ͬ�������ʱ��Ϊ��������| A�� | $\sqrt{\frac{2\sqrt{{L}_{1}{L}_{2}}}{g}}$ | B�� | $\sqrt{\frac{\sqrt{2{L}_{1}{L}_{2}}}{g}}$ | ||
| C�� | $\sqrt{\frac{2\sqrt{{{L}_{1}}^{2}+{{L}_{2}}^{2}}}{g}}$ | D�� | $\sqrt{\frac{2��{{L}_{1}}^{2}+{{L}_{2}}^{2}��}{g��{L}_{1}+{L}_{2}��}}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com