
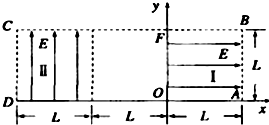
 如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场Ⅰ和Ⅱ,两电场的边界均是边长为L的正方形(不计电子所受重力).
如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场Ⅰ和Ⅱ,两电场的边界均是边长为L的正方形(不计电子所受重力).分析 (1)在AB边的中点处由静止释放电子,电场力对电子做正功,根据动能定理求出电子穿过电场时的速度.进入电场II后电子做类平抛运动,水平方向做匀速直线运动,竖直方向做匀加速直线运动,由牛顿第二定律求出电子的加速度,由运动学公式结合求出电子离开ABCD区域的位置坐标.
(2)在电场I区域内适当位置由静止释放电子,电子先在电场Ⅰ中做匀加速直线运动,进入电场Ⅱ后做类平抛运动,根据牛顿第二定律和运动学公式结合求出位置x与y的关系式
解答 解:(1)电子在区域I中做初速度为零的匀加速直线运动,
根据动能定理可得:eEL=$\frac{1}{2}$mv2∴离开区域I时的速度为v=$\sqrt{\frac{2eEL}{m}}$
电子通过区域I的时间为t1=$\frac{2L}{v}$=$\sqrt{\frac{2mL}{E}}$
电子在区域Ⅱ中匀速运动,通过时用时间为t2=$\frac{L}{v}$=$\sqrt{\frac{mL}{2E}}$
进入区域Ⅲ时电子做类平抛运动,假设电子能穿过CD边,则:
电子在区域Ⅲ运动时间t3=t2=$\frac{L}{v}$=$\sqrt{\frac{mL}{2E}}$
在沿y轴方向上根据牛顿第二定律可得:eE=ma
y轴方向上运动的位移为△y=$\frac{1}{2}$at32=$\frac{L}{4}$<$\frac{L}{2}$,显然假设成立.
电子在ABCD区域内运动经历时间为t=t1+t2+t3=2$\sqrt{\frac{2mL}{E}}$
电子离开时的位移坐标为x=-2L,y=$\frac{L}{2}$-△y=$\frac{L}{4}$
(2)假设释放的位置坐标为(x,y)
在区域I中有:eEL=$\frac{1}{2}$mv2
在区域Ⅲ中有:t=$\frac{L}{v}$
所以y=$\frac{1}{2}$at2=$\frac{eE{L}^{2}}{2m{v}^{2}}$=$\frac{{L}^{2}}{4x}$
所以这些位置在双曲线y=$\frac{{L}^{2}}{4x}$ 上
答:(1)在该区域AB边的中点处由静止释放电子,电子在ABCD区域内运动经历的时间为$2\sqrt{\frac{2mL}{E}}$,电子离开ABCD区域的位置为(-2L,$\frac{L}{4}$);
(2)在电场Ⅰ区域内适当位置由静止释放电子,电子恰能从ABCD区域左下角D处离开,所有释放点的位置为在双曲线y=$\frac{{L}^{2}}{4x}$上
点评 本题实际是加速电场与偏转电场的组合,考查分析带电粒子运动情况的能力和处理较为复杂的力电综合题的能力


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 一个质量m=30g,带电荷量为q=-2×10-8C的半径极小的小球,用丝线悬挂在某匀强电场中,电场线水平.当小球静止时,测得悬线与竖直方向成30°夹角,如图所示,求该电场的场强大小,并说明场强方向.
一个质量m=30g,带电荷量为q=-2×10-8C的半径极小的小球,用丝线悬挂在某匀强电场中,电场线水平.当小球静止时,测得悬线与竖直方向成30°夹角,如图所示,求该电场的场强大小,并说明场强方向.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 火车站广播道:“从广州开往北京的T16次列车将于11点50分到达本站1号站台,停车12分钟,请旅客做好登车准备”,这里的11点50分是指时间 | |
| B. | 第4秒末指的是时间 | |
| C. | 上午第一节课从7:50开始上课,这里的7:50是指时刻 | |
| D. | 在有些情况下,时间就是时刻,时刻就是时间 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 一根轻绳,两端分别固定在竖直棒上相距为L的A、B两点,一个质量为m的光滑小圆环套在绳子上,当竖直棒以一定的角速度转动时,圆环以A为圆心在水平面上做匀速圆周运动,这时轻绳上端与竖直棒成45°夹角,如图所示,求竖直棒转动的角速度.(重力加速度为g)
一根轻绳,两端分别固定在竖直棒上相距为L的A、B两点,一个质量为m的光滑小圆环套在绳子上,当竖直棒以一定的角速度转动时,圆环以A为圆心在水平面上做匀速圆周运动,这时轻绳上端与竖直棒成45°夹角,如图所示,求竖直棒转动的角速度.(重力加速度为g)查看答案和解析>>
科目:高中物理 来源: 题型:多选题

| A. | 入射角大于折射角,声波在介质Ⅰ中的波速大于它在介质Ⅱ中的波速 | |
| B. | 入射角大于折射角,Ⅰ可能是空气,Ⅱ可能是水 | |
| C. | 入射角小于折射角,Ⅰ可能是钢铁,Ⅱ可能是空气 | |
| D. | 介质Ⅰ中波速v1,与介质Ⅱ中波速v2满足:$\frac{{v}_{1}}{{v}_{2}}$=$\frac{sin{θ}_{1}}{sin{θ}_{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com