
 ��ͼ��ʾ�����Ǧ�=45��Ĺ⻬�������� MON�̶���ˮƽ���ڣ����촦�ڷ�����ֱ���Ÿ�Ӧǿ��ΪB����ǿ�ų��У�һ����ON��ֱ�ĵ������ˮƽ�����������Ժ㶨�ٶ�v0�ص���MON���һ����������������Ϊm�������뵼�����λ���ȵĵ������Ϊr��������뵼��Ӵ���Ϊa��b��������ڻ���������ʼ�ձ����뵼�����ýӴ���û�����뵼�죮��t=0ʱ�������λ������ԭ��o������
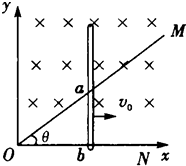
��ͼ��ʾ�����Ǧ�=45��Ĺ⻬�������� MON�̶���ˮƽ���ڣ����촦�ڷ�����ֱ���Ÿ�Ӧǿ��ΪB����ǿ�ų��У�һ����ON��ֱ�ĵ������ˮƽ�����������Ժ㶨�ٶ�v0�ص���MON���һ����������������Ϊm�������뵼�����λ���ȵĵ������Ϊr��������뵼��Ӵ���Ϊa��b��������ڻ���������ʼ�ձ����뵼�����ýӴ���û�����뵼�죮��t=0ʱ�������λ������ԭ��o���������� ��1�����tʱ�̵��������Ч���ȣ�����и�����ĸ�Ӧ�綯�ƺͱպϵ�·ŷķ�����������ǿ�ȵĴ�С���������������ֱ���˶�ʱ��ˮƽ�������ڰ�����������ƽ�����ˮƽ�����ı���ʽ��
��2���������0��tʱ���ڵ�����С�㶨��ץסR��ʱ�����ȣ�ͨ��ƽ�����ʣ�����Q=Pt��������Ľ�����Q��
��3�����ݶ��������������˼�롢�˶�ѧ��ʽ�����t=0ʱ�̽�����F��ȥ������������ڵ����Ͼ�ֹʱ������x
��� �⣺��1��0��tʱ���ڣ��������λ�� x=v0t
tʱ�̣���������� l=x
������ĵ綯�� E=Blv0
��·�ܵ��� R=��2x+$\sqrt{2}$x��r
����ǿ�� I=$\frac{E}{R}$=$\frac{B{v}_{0}}{��2+\sqrt{2}��r}$
���ڵ�����������˶�������������������
�� F=BIl=$\frac{{B}^{2}{v}_{0}^{2}t}{��2+\sqrt{2}��r}$
��2����tʱ�̵�����ĵ��� R=��2+$\sqrt{2}$��rv0t �� R��t
���ڵ���I�㶨����� Q=${I}^{2}\overline{R}t$=$[\frac{B{v}_{0}}{��2+\sqrt{2}r��}]^{2}$•$\frac{{v}_{0}tr}{2}t$=$\frac{{B}^{2}{v}_{0}^{3}{t}^{2}}{2��2+\sqrt{2}��^{2}r}$
��3����ȥ������������ʱ��t�����������Ϊx���ٶ�Ϊv��ȡ����ʱ���t
��t��t+��tʱ���ڣ��ɶ��������� BlI��t=m��v
�ɵ� B$\frac{Bv}{��2+\sqrt{2}��r}$vt��t=$\frac{{B}^{2}��s}{��2+\sqrt{2}��r}$=m��v
��t0��tʱ���� $\sum_{\;}^{\;}$ $\frac{{B}^{2}��s}{��2+\sqrt{2}��r}$=mv0����s��=$\frac{��x+{x}_{0}����x-{x}_{0}��}{2}$=$\frac{{x}^{2}-{x}_{0}^{2}}{2}$
�ɵ� $\frac{{B}^{2}}{��2+\sqrt{2}��r}$•$\frac{{x}^{2}-{x}_{0}^{2}}{2}$=mv0��
���� x0=v0t0��
�������ֹʱ������Ϊ x=$\sqrt{\frac{2��2+\sqrt{2}��rm{v}_{0}}{{B}^{2}}+��{v}_{0}{t}_{0}��^{2}}$
��
��1�������������ֱ���˶�ʱˮƽ����F�ı���ʽΪF=$\frac{{B}^{2}{v}_{0}^{2}t}{��2+\sqrt{2}��r}$��
��2���������0��tʱ���ڲ����Ľ�����QΪ$\frac{{B}^{2}{v}_{0}^{3}{t}^{2}}{2��2+\sqrt{2}��^{2}r}$��
��3������t0ʱ�̽�����F��ȥ������������ڵ����Ͼ�ֹʱ������xΪ$\sqrt{\frac{2��2+\sqrt{2}��rm{v}_{0}}{{B}^{2}}+��{v}_{0}{t}_{0}��^{2}}$��
���� �����ۺϿ������и�����ĸ�Ӧ�綯�ơ��պϵ�·ŷķ���ɡ�ţ�ٵڶ����ɵ�֪ʶ�㣬Ҫע�ⲻ��ֻ���ݸ�Ӧ��綯�Ʊ仯����Ϊ��Ӧ������С����ʵ����Ҳ����Ӧ�������䣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ������磬�����˶� | B�� | �����磬�����˶� | ||
| C�� | ������磬�����˶� | D�� | �����磬�����˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | C��Q������ | B�� | C����Q��С | C�� | C��С��Q���� | D�� | C��Q����С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
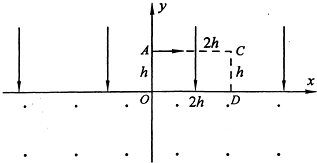
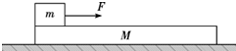 ��ͼ��ʾ���⻬ˮƽ���Ϸ�������ΪM��ľ�壬ľ����ϱ���ֲ��������һ������Ϊm��ľ��?�ֶ�ľ��ʩ��һ��ˮƽ���ҵĺ���F��ľ����ľ���ɾ�ֹ��ʼ�˶�������ʱ��t����?����˵����ȷ���ǣ�������
��ͼ��ʾ���⻬ˮƽ���Ϸ�������ΪM��ľ�壬ľ����ϱ���ֲ��������һ������Ϊm��ľ��?�ֶ�ľ��ʩ��һ��ˮƽ���ҵĺ���F��ľ����ľ���ɾ�ֹ��ʼ�˶�������ʱ��t����?����˵����ȷ���ǣ�������| A�� | ��������ľ�������M����ʱ��t���� | |
| B�� | ��������ľ�������m����ʱ��t���� | |
| C�� | �����������F����ʱ��t���� | |
| D�� | ��������ľ����ľ���Ķ�Ħ����������ʱ��t���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��ABCΪһ���������������ι�ѧԪ���ĺ���棬DΪACԲ����Բ�ģ���ADC=120�㣬��ABC=60�㣬AB=BC��B��D��ľ���Ϊd��D�����Դ�����Ĺ�����һ�����߾�AB��BC��������ȫ�������ǡ��ͨ��D�㣮��
��ͼ��ʾ��ABCΪһ���������������ι�ѧԪ���ĺ���棬DΪACԲ����Բ�ģ���ADC=120�㣬��ABC=60�㣬AB=BC��B��D��ľ���Ϊd��D�����Դ�����Ĺ�����һ�����߾�AB��BC��������ȫ�������ǡ��ͨ��D�㣮���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ijˮ��ˮ��̲�����������ɽɫ����ʫ�续��ˮ����һ��С���������Ž���ֻ����������ͼ������Ϊm��С�����ڵ���ǧ���������ˮƽ����F�������ؽ���ǧ����͵���������ֱ����нǦȣ�������ΪL���ڴ˹�����ȷ���ǣ�������
ijˮ��ˮ��̲�����������ɽɫ����ʫ�续��ˮ����һ��С���������Ž���ֻ����������ͼ������Ϊm��С�����ڵ���ǧ���������ˮƽ����F�������ؽ���ǧ����͵���������ֱ����нǦȣ�������ΪL���ڴ˹�����ȷ���ǣ�������| A�� | ����F�Ǻ��� | B�� | ���нǦȼ�������������ܻ�� | ||
| C�� | ����F����WF=FLsin�� | D�� | ����������������mgLcos�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��һ����m=1.0kg��С��龲ֹ�ڴֲ�ˮƽ̨���ϣ���̨�ױ�ԵO��ľ���s=5m������ˮƽ̨�ױ���Ķ�Ħ��������=0.25����̨���Ҳ�̶�һ����OΪԲ�ĵ� $\frac{1}{4}$Բ�����壬Բ���뾶R=5$\sqrt{2}$m����O��Ϊԭ�㽨��ƽ��ֱ������ϵxOy������F=5N��ˮƽ��������С��飨��֪�������ٶ�g=10m/s2����
��ͼ��ʾ��һ����m=1.0kg��С��龲ֹ�ڴֲ�ˮƽ̨���ϣ���̨�ױ�ԵO��ľ���s=5m������ˮƽ̨�ױ���Ķ�Ħ��������=0.25����̨���Ҳ�̶�һ����OΪԲ�ĵ� $\frac{1}{4}$Բ�����壬Բ���뾶R=5$\sqrt{2}$m����O��Ϊԭ�㽨��ƽ��ֱ������ϵxOy������F=5N��ˮƽ��������С��飨��֪�������ٶ�g=10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ���뾶R=0.4m�Ĺ⻬Բ������̶�����ֱƽ���ڣ������һ���˵�B��Բ��O��������ˮƽ�����ļнǦ�=30�㣬��һ�˵�CΪ�������͵㣬C���Ҳ�Ĺ⻬ˮƽ·���Ͻ���C�����һľ�壬ľ������M=2kg���ϱ�����C��ȸߣ�����m=1kg����飨����Ϊ�ʵ㣩�ӿ���A����v0=1m/s���ٶ�ˮƽ�׳���ǡ�ôӹ����B�������߷�����������ع������֮���ֻ���ľ�壬��ľ���ľ���Ҷ˻���ʱ���ٶ�Ϊv1=2m/s����֪�����ľ���Ķ�Ħ��������=0.5��ȡg=10m/s2����
��ͼ��ʾ���뾶R=0.4m�Ĺ⻬Բ������̶�����ֱƽ���ڣ������һ���˵�B��Բ��O��������ˮƽ�����ļнǦ�=30�㣬��һ�˵�CΪ�������͵㣬C���Ҳ�Ĺ⻬ˮƽ·���Ͻ���C�����һľ�壬ľ������M=2kg���ϱ�����C��ȸߣ�����m=1kg����飨����Ϊ�ʵ㣩�ӿ���A����v0=1m/s���ٶ�ˮƽ�׳���ǡ�ôӹ����B�������߷�����������ع������֮���ֻ���ľ�壬��ľ���ľ���Ҷ˻���ʱ���ٶ�Ϊv1=2m/s����֪�����ľ���Ķ�Ħ��������=0.5��ȡg=10m/s2�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com