
| A. | 月球绕地球的半径的三次方与周期的平方比等于火星绕太阳的半径的三次方与周期的平方比 | |
| B. | 某颗地球卫星的周期可能是1.2h | |
| C. | 卫星运动的角速度与卫星质量无关 | |
| D. | 周期是24h的卫星一定是地球同步卫星 |
分析 根据开普勒第三定律分析月球绕地球的半径的三次方与周期的平方比和火星绕太阳的半径的三次方与周期的平方比的关系.地球卫星的周期最小是近地卫星的周期,可根据第一宇宙速度和地球半径估算.卫星运动的角速度与卫星质量无关.根据地球同步卫星的条件分析即可.
解答 解:A、根据开普勒第三定律$\frac{{R}^{3}}{{T}^{2}}$=k知,k与中心天体的质量有关,所以月球绕地球的半径的三次方与周期的平方比与地球的质量有关,火星绕太阳的半径的三次方与周期的平方比与太阳的质量有关,两个比值不等,故A错误.
B、近地卫星的线速度为:v=7.9×103m/s,
轨道半径约等于地球半径为:R=6400km=6400×103,
其周期为:T=$\frac{2πR}{v}$=$\frac{2×3.14×6400×1{0}^{3}}{7.9×1{0}^{3}}$s≈5088s≈1.4h
由开普勒第三定律知,地球卫星的周期最小为1.4h,不可能为1.2h,故B错误.
C、根据万有引力提供向心力,有:G$\frac{Mm}{{r}^{2}}$=mω2r,
得:ω=$\sqrt{\frac{GM}{{r}^{3}}}$,可知卫星运动的角速度与卫星质量m无关,故C正确.
D、周期是24小时的卫星,不一定在赤道的正上方,所以不一定是同步卫星,故D错误;
故选:C
点评 解决本题的关键是掌握开普勒第三定律和万有引力等于向心力这一基本思路.要明确地球同步卫星必须满足两个条件:1、必须定点于赤道正上方.2、周期必须与地球自转周期相同.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:高中物理 来源: 题型:计算题
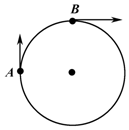 一物体沿半径为10m的圆形轨道在水平面内做匀速圆周运动,线速度为10m/s,在A点运动方向为正北,经$\frac{1}{4}$周期运动至B点,在B点运动方向为正东,如图所示,求:
一物体沿半径为10m的圆形轨道在水平面内做匀速圆周运动,线速度为10m/s,在A点运动方向为正北,经$\frac{1}{4}$周期运动至B点,在B点运动方向为正东,如图所示,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图1所示,以v0=10m/s的水平速度抛出一物体,不计空气阻力,飞行一段时间后,垂直的撞在倾角为30°的斜面上.物体完成这段飞行的时间是( )
如图1所示,以v0=10m/s的水平速度抛出一物体,不计空气阻力,飞行一段时间后,垂直的撞在倾角为30°的斜面上.物体完成这段飞行的时间是( )| A. | $\sqrt{3}s$ | B. | 2s | C. | $\frac{{\sqrt{3}}}{3}s$ | D. | $\frac{{2\sqrt{3}}}{3}s$ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
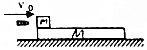 如图所示,质量为M的木板房在光滑水平面上,其左端放置一个质量为m的小滑块,开始时二者均处于静止状态,现有一质量为m0的子弹以水平速度v0击中滑块并留在其中,已知木板足够长,小滑块与木板之间的动摩擦因数为μ,求小滑块在木板上滑过的距离.
如图所示,质量为M的木板房在光滑水平面上,其左端放置一个质量为m的小滑块,开始时二者均处于静止状态,现有一质量为m0的子弹以水平速度v0击中滑块并留在其中,已知木板足够长,小滑块与木板之间的动摩擦因数为μ,求小滑块在木板上滑过的距离.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 若地面光滑,人和车组成的系统总动量方向与小车运动方向相同 | |
| B. | 若地面光滑,人和车组成的系统动量守恒 | |
| C. | 无论地面是否光滑,人和车组成的系统动量都一定守恒 | |
| D. | 只有当人的质量远远小于车的质量时,人和车组成的系统动量才守恒 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,水平面上OM正中间有质量分别为2m、m的两物块B、C(中间粘有少量炸药),现引爆炸药,B、C被水平弹开,物块C运动到O点时,与刚好到达该点、质量为m、速度大小为v0的小物块A发生迎面正碰,碰后两者结合为一体向左滑动并刚好在M点与B相碰.不计一切摩擦,不计物体碰撞时间,三物块均可视为质点,重力加速度g=10m/s2.求:
如图所示,水平面上OM正中间有质量分别为2m、m的两物块B、C(中间粘有少量炸药),现引爆炸药,B、C被水平弹开,物块C运动到O点时,与刚好到达该点、质量为m、速度大小为v0的小物块A发生迎面正碰,碰后两者结合为一体向左滑动并刚好在M点与B相碰.不计一切摩擦,不计物体碰撞时间,三物块均可视为质点,重力加速度g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
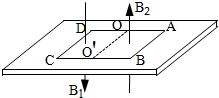 如图所示为磁悬浮列车模型,质量M=1.5kg的绝缘板底座与水平地面的动摩擦因数μ=0.1,正方形金属框ABCD固定在绝缘底座,其质量m=0.5kg,边长为1m,电阻为$\frac{1}{16}$Ω.OOˊ为AD、BC的中点.在金属框内有可随金属框同步移动的磁场,OOˊCD区域内磁场B1=kt,且k=0.5T/s,方向竖直向下;OOˊBA区域内磁场B2=2T,方向竖直向上.若AB恰在磁场边缘以内,CD边恰在磁场边缘以外,静止释放模型后,其加速度为3m/s2;若AB边和CD边恰都在磁场边缘以内,静止释放模型后,经过4s速度达到20m/s.(重力加速度g取10m/s2)
如图所示为磁悬浮列车模型,质量M=1.5kg的绝缘板底座与水平地面的动摩擦因数μ=0.1,正方形金属框ABCD固定在绝缘底座,其质量m=0.5kg,边长为1m,电阻为$\frac{1}{16}$Ω.OOˊ为AD、BC的中点.在金属框内有可随金属框同步移动的磁场,OOˊCD区域内磁场B1=kt,且k=0.5T/s,方向竖直向下;OOˊBA区域内磁场B2=2T,方向竖直向上.若AB恰在磁场边缘以内,CD边恰在磁场边缘以外,静止释放模型后,其加速度为3m/s2;若AB边和CD边恰都在磁场边缘以内,静止释放模型后,经过4s速度达到20m/s.(重力加速度g取10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,三个滑块A、B、C静置于同一光滑水平轨道上,滑块B、C的质量均为0.7kg,现给滑块A向右的初速度v0,一段时间后A与B发生碰撞,碰后A、B分别以$\frac{1}{8}$v0、$\frac{3}{4}$v0的速度向右运动,B再与C发生碰撞,碰后B、C粘在一起向右运动,两次碰撞时间极短.
如图所示,三个滑块A、B、C静置于同一光滑水平轨道上,滑块B、C的质量均为0.7kg,现给滑块A向右的初速度v0,一段时间后A与B发生碰撞,碰后A、B分别以$\frac{1}{8}$v0、$\frac{3}{4}$v0的速度向右运动,B再与C发生碰撞,碰后B、C粘在一起向右运动,两次碰撞时间极短.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com