
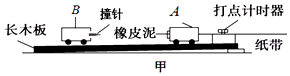

���� С��������ֱ���˶�ʱ�������ʱ����С����λ����ȣ�����ֽ��������ֽ����������ٶȣ��ٸ��ݶ����Ķ�����������ײǰ��Ķ�����С���Ӷ���֤�����Ƿ��غ㣮
��� �⣺��1���ƶ�С���ɾ�ֹ��ʼ�˶�����С���и����ٹ��̣�����ײǰ������ֱ���˶���������ͬ��ʱ����ͨ����λ����ͬ����BC��Ϊ�����˶��ĽΣ���ѡBC������ǰ���ٶȣ�
��ײ������һ�������˶��Ĺ��̣���A��B����Ĺ�ͬ�˶�ʱ������ֱ���˶���������ͬ��ʱ����ͨ����ͬ��λ�ƣ���ӦѡDE������������ͬ���ٶȣ�
��2����ͼ��֪��BC=31.50cm=0.3150m��
DE=20.85cm=0.2085m��
A��ǰ���ٶȣ�v1=$\frac{BC}{t}$=$\frac{0.3150}{5��0.02}$=3.15m/s
����ͬ�ٶȣ�v2=$\frac{DE}{t}$=$\frac{0.2085}{5��0.02}$=2.085m/s
��ǰ�ܶ�����P1=m1v1=0.4��3.15=1.26kgm/s
������ܶ�����P2=��m1+m2��v2=0.6��2.085=1.25kgm/s
��˵������������ķ�Χ�ڣ���ײǰ���ܶ����غ�
�ʴ�Ϊ����1��BC�� DE����2��1.26�� 1.25�� ����������ķ�Χ�ڣ���ײǰ���ܶ����غ�
���� ���⿼����֤�����غ㶨�ɵ�ʵ��ԭ����Ҫע��������Ĺؼ�֪��A��B�����ٶȼ�С����ͨ��ֽ������ٶȵĴ�С����ͨ����ײǰ��Ķ�����С��ϵ��֤�����Ƿ���ȼ��ɣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����

| A�� | �ü�г�����ݲ� | B�� | �ü�г�������Ϊ2L | ||
| C�� | t=$\frac{T}{8}$ʱ��P��ƽ��λ���Ϸ� | D�� | t=$\frac{3T}{8}$ʱ��P���ٶȷ�����ֱ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
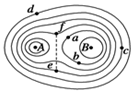 λ��A��B�����������в���������ĵ�����ƽ���ڵ��Ʒֲ���ͼ��ʾ��ͼ��ʵ�߱�ʾ�����ߣ�������
λ��A��B�����������в���������ĵ�����ƽ���ڵ��Ʒֲ���ͼ��ʾ��ͼ��ʵ�߱�ʾ�����ߣ�������| A�� | a���b��ĵ糡ǿ����ͬ | |
| B�� | c��d������Ʋ����0 | |
| C�� | ����ɴ�a���Ƶ�c�㣬�糡�������� | |
| D�� | ����ɴ�e����ͼ�������Ƶ�f��������ȼ�С������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ������ѹ������ѧ�¶ȳ����� | |
| B�� | һ���������������ڵ��������������յ��������ڶ������Ĺ�������Υ������ѧ�ڶ����� | |
| C�� | �����Ӽ�����������ƽ��ʱ��������һ��Ϊ�㣬��������һ����С | |
| D�� | �����¶�Խ�ߣ���������˶�Խ���ҡ��������ܵ��ij����Խ�������ѹǿԽ�� | |
| E�� | ���κ���Ȼ�����У�һ������ϵͳ�е����ز������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
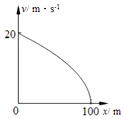 С�����ڴֲڵ�ˮƽ���ϣ���A���������������¿�ʼ������ֱ���˶�������B���Ժ����ڳ�ȥ���������ȼ���ֱ���˶�������C��ͣ��������֪BC�����ȼ���ֱ���˶���λ��x���ٶ�v�Ĺ�ϵͼ����ͼ��ʾ��A��C����֮��ľ���Ϊ400m��������
С�����ڴֲڵ�ˮƽ���ϣ���A���������������¿�ʼ������ֱ���˶�������B���Ժ����ڳ�ȥ���������ȼ���ֱ���˶�������C��ͣ��������֪BC�����ȼ���ֱ���˶���λ��x���ٶ�v�Ĺ�ϵͼ����ͼ��ʾ��A��C����֮��ľ���Ϊ400m��������| A�� | B��C����֮��ľ���Ϊ200 m | |
| B�� | BC �����ȱ����˶��ļ��ٶȴ�СΪ4 m/s2 | |
| C�� | AB �������˶�����ʱ��Ϊ10 s | |
| D�� | AC ����������ʱ��Ϊ25 s |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
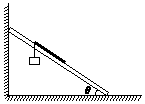 ľ��̶���ǽ�Ǵ�����ˮƽ��н�Ϊ��=37�㣬ľ���ϱ���⻬��ľ���Ͽ���һ������һ����Ϊl������Ϊm����������ľ���ϣ����϶˸պý��������ϸ�߽�����Ϊm��������������ӣ���ͼ��ʾ������ɾ�ֹ�ͷź������˶����������������˶����������պ�ȫ���뿪ľ�壨��ʱ���δ������棩ʱ�������ٶ�Ϊ����֪�������ٶ�Ϊg��sin 37��=0.6����������
ľ��̶���ǽ�Ǵ�����ˮƽ��н�Ϊ��=37�㣬ľ���ϱ���⻬��ľ���Ͽ���һ������һ����Ϊl������Ϊm����������ľ���ϣ����϶˸պý��������ϸ�߽�����Ϊm��������������ӣ���ͼ��ʾ������ɾ�ֹ�ͷź������˶����������������˶����������պ�ȫ���뿪ľ�壨��ʱ���δ������棩ʱ�������ٶ�Ϊ����֪�������ٶ�Ϊg��sin 37��=0.6����������| A�� | $\sqrt{gl}$ | B�� | $\sqrt{1.1gl}$ | C�� | $\sqrt{1.2gl}$ | D�� | $\sqrt{2gl}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $m{g_0}{R^2}��{\frac{1}{R_2}-\frac{1}{R_1}}��$ | B�� | $mg{R^2}��{\frac{1}{R_2}-\frac{1}{R_1}}��$ | ||
| C�� | $\frac{{mg{R^2}}}{2}��{\frac{1}{R_2}-\frac{1}{R_1}}��$ | D�� | $\frac{{m{g_0}{R^2}}}{2}��{\frac{1}{R_2}-\frac{1}{R_1}}��$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �����˶������ʼ�С | B�� | �����˶��Ľ��ٶȱ�� | ||
| C�� | �����˶������ڱ�� | D�� | ���ǵ����ļ��ٶȱ�С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ���ʵ�a��b��ֱ��PQ�ϵ������˵㣬�ʵ�a��P��PQ�����ٶ�Ϊ0���ȼ���ֱ���˶�������λ��x1ʱ�ʵ�b��Q��QP���������ٶ�Ϊ0���ȼ���ֱ���˶���λ��x2ʱ���ʵ�a���������ʵ�ļ��ٶȴ�С��ͬ����PQ����Ϊ��������
��ͼ��ʾ���ʵ�a��b��ֱ��PQ�ϵ������˵㣬�ʵ�a��P��PQ�����ٶ�Ϊ0���ȼ���ֱ���˶�������λ��x1ʱ�ʵ�b��Q��QP���������ٶ�Ϊ0���ȼ���ֱ���˶���λ��x2ʱ���ʵ�a���������ʵ�ļ��ٶȴ�С��ͬ����PQ����Ϊ��������| A�� | x1+2x2+2$\sqrt{{x}_{1}{x}_{2}}$ | B�� | 2x1+x2+2$\sqrt{{x}_{1}{x}_{2}}$ | C�� | x1+2x2+$\sqrt{2{x}_{1}{x}_{2}}$ | D�� | 2x1+x2+$\sqrt{2{x}_{1}{x}_{2}}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com