
| A. | 求出月球的质量 | B. | 求出“嫦娥三号”探月卫星的质量 | ||
| C. | 得出$\frac{{{r}_{1}}^{3}}{{{T}_{1}}^{2}}$=$\frac{{{r}_{2}}^{3}}{{{T}_{2}}^{2}}$ | D. | 求出地球的密度 |
分析 分别以月球和“嫦娥三号”为研究对象,根据万有引力提供向心力列式,可求得月球和地球的质量.由于地球本身的半径未知,是不能求出地球的密度的
解答 解:A、B“嫦娥三号”探月卫星做圆周运动的环月轨道半径为r2、周期为T2,由月球的万有引力提供向心力,则有:
$G\frac{{M}_{月}^{\;}{m}_{嫦}^{\;}}{{r}_{2}^{2}}={m}_{嫦}^{\;}\frac{4{π}_{\;}^{2}}{{T}_{2}^{2}}{r}_{2}^{\;}①$
则得:${M}_{月}^{\;}=\frac{4{π}_{\;}^{2}{r}_{2}^{3}}{G{T}_{2}^{2}}$②
可知能求出月球的质量,根据题目条件不能求出“嫦娥三号”探月卫星的质量,故A正确,B错误.
C、同理,月球绕地球做圆周运动,由地球的万有引力提供向心力,则有:
$G\frac{{M}_{地}^{\;}{m}_{月}^{\;}}{{r}_{1}^{2}}={m}_{月}^{\;}\frac{4{π}_{\;}^{2}}{{T}_{1}^{2}}{r}_{1}^{2}$③
则得:${M}_{地}^{\;}=\frac{4{π}_{\;}^{2}{r}_{1}^{3}}{G{T}_{1}^{2}}$④
由②④知$\frac{{r}_{1}^{3}}{{T}_{1}^{2}}=\frac{{r}_{2}^{3}}{{T}_{2}^{2}}$是错误的;也可以由开普勒第三定律直接得到,因为不是同一中心天体,所以$\frac{{r}_{1}^{3}}{{T}_{1}^{2}}≠\frac{{r}_{2}^{3}}{{T}_{2}^{2}}$,故C错误
D、由于地球的半径未知,不能求出地球的体积,就不能求出地球的密度,故D错误.
故选:A.
点评 本题是典型的天体运动的问题,根据万有引力提供向心力是解决这类问题的基本思路,要知道知道环绕天体的轨道半径和周期,能求出中心天体的质量,而不能求出环绕天体的质量.


科目:高中物理 来源: 题型:多选题
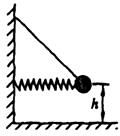 用细绳拴一个质量为m的小球,小球将固定在墙上的轻弹簧压缩的距离为x,不计空气阻力.如图所示,将细线烧断后( )
用细绳拴一个质量为m的小球,小球将固定在墙上的轻弹簧压缩的距离为x,不计空气阻力.如图所示,将细线烧断后( )| A. | 小球立即做平抛运动 | B. | 小球落地时动能大于mgh | ||
| C. | 小球脱离弹簧后做匀变速运动 | D. | 刚烧断后的瞬间小球的加速度为g |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 月球对“嫦娥三号”卫星的吸引力 | B. | 月球的质量 | ||
| C. | “嫦娥三号”卫星绕月运行的速度 | D. | 月球的第一宇宙速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 地球绕太阳运行的周期T地及地日中心间的距离r日地 | |
| B. | 月球绕地球运行的周期T月及地日中心间的距离r月地 | |
| C. | 人造地球卫星在地面附近绕行时的运行周期T | |
| D. | 若不考虑地球的自转,已知地球的半径R和地球表面的重力加速度g |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 匀速圆周运动是速度大小不变的匀变速曲线运动 | |
| B. | 开普勒利用扭称实验了万有引力常量的数值 | |
| C. | 行星绕恒星运动轨道为圆形,则它运动的周期平方与轨道半径的三次方之比$\frac{{T}^{2}}{{R}^{3}}$=K为常数,此常数的大小与恒星的质量和行星的速度有关 | |
| D. | 牛顿发现了万有引力定律 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 10-13N | B. | 10-9N | C. | 10-5 N | D. | 10-1N |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com