
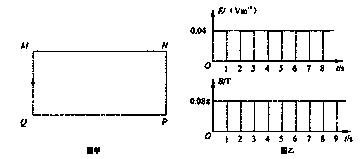
如图甲所示,在整个矩形区域MNPQ内有由M指向N方向的匀强电场E(图甲中未画出)和垂直矩形区域向外的匀强磁场B(图甲中未画出),E和B随时间变化的规律如图乙所示在t=0时刻,将带正电、比荷为25C/kg的粒子从MQ的中点无初速释放,粒子在第8s内经NP边离开矩形区域已知MQ边足够长,粒子重力不计,![]() 。
。
(1)求矩形区域PQ边长满足的条件;
(2)若要粒子从MQ边飞出,释放粒子的时刻t应满足什么条件?
解:(1)第1s内粒子在电场力的作用下作匀加速直线运动,设加速度为a,由牛顿第二定律有:
![]() ①(1分)
①(1分)
第2s内粒子在库仑力作用下作匀速圆周运动,有:
![]() ②(1分)
②(1分)
代入已知数据可得T=1s,所以可得粒子在1s、3s、5s、7s内作匀加速运动,2s,4s,6s内作匀速圆周运动。 (1分)
可作出粒子在第8s内刚好不从NP边离开矩形区域的运动示意图,如图所示。粒子在奇数秒内的整体运动可以等效为初速度为0的匀加速直线运动。 (1分)
设前7s内的位移为s7,
![]() ③(1分)
③(1分)
设粒子第7s末的速度为υ7,第8s内粒子圆周运动的半径为R8,有:
υ7=a(7-3) (1分)
![]() ④(1分)
④(1分)
由图可知,粒子要在第8s内从NP边离开矩形区域,要满足
![]() ⑤(2分)
⑤(2分)
由以上各式联立求解,可得:8m<LNP<8.64m (2分)
(2)设在第1秒内的t0时刻释放粒子,则第1s内粒子在电场力的作用下加速时间为1-t0,第1s内的位移为s0,第1s末的速度大小为υ0,由运动学方程有:
![]() ⑥(1分)
⑥(1分)
υ0=a(1-t0) ⑦(1分)
粒子在磁场中作匀速圆周运动,设圆周运动的半径为r0,有:
![]() ⑧(1分)
⑧(1分)
要粒子从MQ边界飞出,则r0>s0 ⑨(2分)
由⑥~⑨式可得:t>0.68s (1分)
结合电场和磁场的周期性可得要粒子从MN边飞出,粒子释放的时刻t满足:
(2n+0.68)s<t<(2n+1)s (n∈N) (2分)
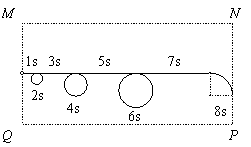


科目:高中物理 来源: 题型:阅读理解
 2004年1月,我国月球探测工程经国务院正式批准立项后,该工程被命名为“嫦娥工程”,整个探月工程将分为三期完成,要突破“绕”、“落”和“回”三大关键技术.第一颗绕月卫星命名为“嫦娥一号”,并且“嫦娥二号”于2010年10月1日18时59分57秒在西昌卫星发射中心发射升空,并获得了圆满成功.
2004年1月,我国月球探测工程经国务院正式批准立项后,该工程被命名为“嫦娥工程”,整个探月工程将分为三期完成,要突破“绕”、“落”和“回”三大关键技术.第一颗绕月卫星命名为“嫦娥一号”,并且“嫦娥二号”于2010年10月1日18时59分57秒在西昌卫星发射中心发射升空,并获得了圆满成功.| R | r |
查看答案和解析>>
科目:高中物理 来源: 题型:
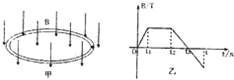
 如图甲所示,在一个正方形金属线圈区域内,存在着磁感应强度B随时间变化的匀强磁场,磁场的方向与线圈平面垂直.金属线圈所围的面积S=200cm2,匝数n=1000,线圈电阻r=1.0Ω.线圈与电阻R构成闭合回路,电阻的阻值R=4.0Ω.匀强磁场的磁感应强度随时间变化的情况如图乙所示,求:
如图甲所示,在一个正方形金属线圈区域内,存在着磁感应强度B随时间变化的匀强磁场,磁场的方向与线圈平面垂直.金属线圈所围的面积S=200cm2,匝数n=1000,线圈电阻r=1.0Ω.线圈与电阻R构成闭合回路,电阻的阻值R=4.0Ω.匀强磁场的磁感应强度随时间变化的情况如图乙所示,求:查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
| 1 | π |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com