
分析 (1)带电质点在电场与磁场中做匀速圆周运动,则电场力与重力相平衡,而洛伦兹力提供向心力,由牛顿第二定律即可求解.
(2)根据质点做匀速直线运动,质点受力平衡,从而依据几何关系可求出电场强度大小及其方向;
(3)当撤去磁场后,带电质点只受电场力和重力作用,在这个过程中电场力不做功,由机械能守恒定律可求出M、N两点间的竖直高度H;由质点做类平抛运动将其速度分解与功率表达式相结合,从而确定经过N点时重力做功的功率.
解答 解:(1)由于带电质点在重力场、匀强电场${E}_{1}^{\;}$和匀强磁场${B}_{1}^{\;}$共存的区域做匀速圆周运动,所以受到的电场力必定与重力平衡,即$q{E}_{1}^{\;}=mg$
解得${E}_{1}^{\;}$=$\frac{mg}{q}$,由质点带负电可知${E}_{1}^{\;}$方向竖直向下
根据牛顿第二定律和向心力公式:$q{v}_{0}^{\;}{B}_{1}^{\;}=m\frac{{v}_{0}^{2}}{R}$
解得:${B}_{1}^{\;}=\frac{m{v}_{0}^{\;}}{qR}$
磁感应强度${B}_{1}^{\;}$可能为竖直向上或竖直向下
(2)磁场${B}_{2}^{\;}$和电场${E}_{2}^{\;}$方向相同时,如图甲所示:磁场B和电场E方向相反时,如图乙所示
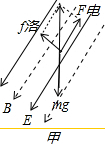
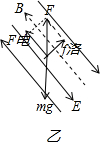
由于带电质点做匀速直线运动,由平衡条件和几何关系可知:
$(q{v}_{0}^{\;}{B}_{2}^{\;})_{\;}^{2}$+$(q{E}_{2}^{\;})_{\;}^{2}$=$(mg)_{\;}^{2}$
解得:${E}_{2}^{\;}=\frac{1}{q}\sqrt{{m}_{\;}^{2}{g}_{\;}^{2}-{q}_{\;}^{2}{v}_{0}^{2}{B}_{2}^{2}}$
图中的θ角由$sinθ=\frac{q{v}_{0}^{\;}{B}_{2}^{\;}}{mg}$
得:$θ=arcsin\frac{q{v}_{0}^{\;}{B}_{2}^{\;}}{mg}$
即电场${E}_{2}^{\;}$的方向为与竖直方向夹角$θ=arcsin\frac{q{v}_{0}^{\;}{B}_{2}^{\;}}{mg}$,且斜向下的一切方向
或:θ=$arctan\frac{q{v}_{0}^{\;}{B}_{2}^{\;}}{q{E}_{2}^{\;}}$=arctan$\frac{q{v}_{0}^{\;}{B}_{2}^{\;}}{\sqrt{{m}_{\;}^{2}{g}_{\;}^{2}-{q}_{\;}^{2}{v}_{0}^{2}{B}_{2}^{2}}}$,且斜向下的一切方向
(3)当撤去磁场后,带电质点只受电场力和重力作用,这两个力的合力大小为$q{v}_{0}^{\;}{B}_{2}^{\;}$,方向既垂直于初速度${v}_{0}^{\;}$的方向也垂直电场${E}_{2}^{\;}$的方向.设空中M、N两点间的竖直高度为H,因为带电质点始终在垂直电场力的平面内运动,故电场力在这个过程中不做功.
则由机械能守恒定律得:$\frac{1}{2}m{v}_{\;}^{2}=mgH+\frac{1}{2}m{v}_{0}^{2}$
解得:$H=\frac{{v}_{\;}^{2}-{v}_{0}^{2}}{2g}$
因带电质点做类平抛运动,由速度的分解可求得带电质点到达N点时沿合力方向的分速度大小为:
${v}_{N}^{\;}=\sqrt{{v}_{\;}^{2}-{v}_{0}^{2}}$
又因电场力在这个过程中不做功,只有重力做功,带电质点到达N点时,重力做功的功率等于合外力在此时的瞬时功率.
解得:${P}_{N}^{\;}=q{v}_{0}^{\;}{B}_{2}^{\;}{v}_{N}^{\;}=q{v}_{0}^{\;}{B}_{2}^{\;}\sqrt{{v}_{\;}^{2}-{v}_{0}^{2}}$
答:(1)要使带电质点进入真空室后做半径为R的匀速圆周运动,此时的电场强度${E}_{1}^{\;}$为$\frac{mg}{q}$,方向竖直向下;磁感应强度B0的大小$\frac{m{v}_{0}^{\;}}{qR}$,所有可能的方向可能竖直向上或竖直向下;
(2)为保证带电质点进入真空室后做匀速直线运动,调整磁场和电场的大小和方向,仍保证电场和磁场方向始终平行,当磁场强度大小变为B2时,此时电场强度E2的大小为$\frac{1}{q}\sqrt{{m}_{\;}^{2}{g}_{\;}^{2}-{q}_{\;}^{2}{v}_{0}^{2}{B}_{2}^{2}}$,方向方向为与竖直方向夹角$θ=arcsin\frac{q{v}_{0}^{\;}{B}_{2}^{\;}}{mg}$,且斜向下的一切方向;
(3)若带电质点在满足第(2)问的条件下运动到空中某一位置M点时立即撤去磁场,此后运动到空中另一位置N点时的速度大小为v,M、N两点间的竖直高度H为$\frac{{v}_{\;}^{2}-{v}_{0}^{2}}{2g}$,经过N点时重力做功的功率$q{v}_{0}^{\;}{B}_{2}^{\;}\sqrt{{v}_{\;}^{2}-{v}_{0}^{2}}$.
点评 考查洛伦兹力提供向心力做匀速圆周运动的处理方法,由洛伦兹、电场力与重力相平衡,结合几何关系来综合求解;同时还考查机械能守恒定律,及类平抛运动规律,并运用功率的表达式来求解.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中物理 来源: 题型:实验题
 ①某同学用在实验室做“单摆的周期T与摆长L的关系”实验,下列措施中可以提高实验精度的是ABC
①某同学用在实验室做“单摆的周期T与摆长L的关系”实验,下列措施中可以提高实验精度的是ABC查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,一质点做匀加速直线运动,先后经过A、B两点,已知A、B两点间距为d,质点在A、B两点间历时t,通过B点时速度大小为v,求:
如图所示,一质点做匀加速直线运动,先后经过A、B两点,已知A、B两点间距为d,质点在A、B两点间历时t,通过B点时速度大小为v,求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 μ子与氢原子核(质子)构成的原子称为μ氢原子(bydrogen muonatom).它在原子核物理的研究中有重要作用.图为μ氢原子的能级示意图,假定光子能量为E的一束光照射容器中大量处于n=2能级的μ氢原子,μ氢原子吸收光子后,发出频率为v1、v2、v3、v4、v5和v6的光,且频率依次增大,则( )
μ子与氢原子核(质子)构成的原子称为μ氢原子(bydrogen muonatom).它在原子核物理的研究中有重要作用.图为μ氢原子的能级示意图,假定光子能量为E的一束光照射容器中大量处于n=2能级的μ氢原子,μ氢原子吸收光子后,发出频率为v1、v2、v3、v4、v5和v6的光,且频率依次增大,则( )| A. | μ氢原子吸收光子后处于n=5能级 | B. | μ氢原子吸收光子后处于n=4能级 | ||
| C. | E等于h(v6-v4) | D. | E等于h(v5-v2) |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | β衰变现象说明电子是原子核的组成部分 | |
| B. | 波尔理论的假设之一是原子能量的量子化 | |
| C. | 放射性元素的半衰期随温度的升高而变短 | |
| D. | 比结合能越小表示原子核中的核子结合得越牢固 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 磁感应强度的方向就是置于该点的小磁针南极受力的方向 | |
| B. | 磁感应强度的方向就是置于该点的电流元所受的安培力的方向 | |
| C. | 某电流元不受安培力,说明该处磁感应强度一定为零 | |
| D. | 磁感应强度的大小和方向由某点磁场本身决定,跟置于该点的电流元无关 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
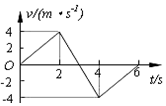
| A. | 6s内物体做匀变速直线运动 | |
| B. | 2~4s内物体做匀变速直线运动 | |
| C. | 2s末物体的速度为4m/s,且改变运动方向 | |
| D. | 3s末物体的速度大小为零,加速度为-4 m/s2 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,在光滑水平面上使滑块A以2m/s的速度向右运动,滑块B以4m/s的速度向左运动并与滑块A发生碰撞,已知滑块A、B的质量分别为1kg、2kg,滑块B的左侧连有轻弹簧,求:
如图所示,在光滑水平面上使滑块A以2m/s的速度向右运动,滑块B以4m/s的速度向左运动并与滑块A发生碰撞,已知滑块A、B的质量分别为1kg、2kg,滑块B的左侧连有轻弹簧,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com