
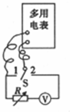
 ����ͼʾ��·���Բ������õ���ڵ�صĵ綯��E��ŷķ����100�����ڲ���·���ܵ���r���ṩ�������У����е������ѹ��������3V�����輸ǧŷ���������䣨0��9999.9����������˫������S���������ɣ���Ҫʵ�鲽�����£��벹��������
����ͼʾ��·���Բ������õ���ڵ�صĵ綯��E��ŷķ����100�����ڲ���·���ܵ���r���ṩ�������У����е������ѹ��������3V�����輸ǧŷ���������䣨0��9999.9����������˫������S���������ɣ���Ҫʵ�鲽�����£��벹������������ ��1������ŷķ����ʹ�÷���������ȷӦ���õIJ��裻
��2�����ݱպϵ�·ŷķ���ɽ�����ʽ�����Σ�������ѧ���ɿ���ȷ�綯�ƺ��ڵ��裮
��� �⣺��1����ʹ��ŷķ��ʱ��ÿ�λ�����Ҫ�Զ��õ������ŷķ���㣻
��3�����ݱպϵ�·ŷķ���ɿ�֪��
U=$\frac{E}{R+r+{R}_{0}}R$
���οɵã�
$\frac{1}{U}$=$\frac{1}{E}$+$\frac{{R}_{0}+r}{E}\frac{1}{R}$
���֪ͼ��Ľؾ�b=$\frac{1}{E}$
��E=$\frac{1}{b}$��
ͼ���б��k=$\frac{{R}_{0}+r}{E}$
��ã�r=$\frac{k}{b}-{R}_{0}$
�ʴ�Ϊ����1��ŷķ���㣻��2��$\frac{1}{b}$�� $\frac{k}{b}-{R}_{0}$
���� ���⿼������綯�ƺ��ڵ����ʵ�飬Ҫע����ȷʵ��ԭ����֪�����õ����ʹ�÷�������ע������������ѡ��պϵ�·ŷķ���ɱ���ʽ���з�����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� | 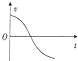 | D�� | 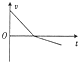 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 ��ͼ��ʾ�������Ϊ����ABCD�����壬�߳�Ϊa�����С�A=60�㣬����һ�����ߴ���A�����$\frac{a}{4}$����P�㴹ֱAB���룬���������AD��ǡ�÷���ȫ���䣬��
��ͼ��ʾ�������Ϊ����ABCD�����壬�߳�Ϊa�����С�A=60�㣬����һ�����ߴ���A�����$\frac{a}{4}$����P�㴹ֱAB���룬���������AD��ǡ�÷���ȫ���䣬���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ��һ�뾶ΪR���ֲڳ̶ȴ�����ͬ�İ�Բ�ι����ֱ�̶����ã�ֱ��POQˮƽ������ϵ�A����PQ�ľ���Ϊ$\frac{1}{2}$R��һ����Ϊm���ʵ���P�����Ϸ�����P���h=2R�ɾ�ֹ�ͷţ���������պ��ܵ���Q�㲢���ٴη��ؾ���N�㣮��֪�ʵ��һ�λ��������͵�Nʱ����Ϊv1����һ�ε���A��ʱ����Ϊv2��ѡ��N�����ڵ�ˮƽ��Ϊ�������ܵ��������棬�������ٶ�Ϊg��������
��ͼ��ʾ��һ�뾶ΪR���ֲڳ̶ȴ�����ͬ�İ�Բ�ι����ֱ�̶����ã�ֱ��POQˮƽ������ϵ�A����PQ�ľ���Ϊ$\frac{1}{2}$R��һ����Ϊm���ʵ���P�����Ϸ�����P���h=2R�ɾ�ֹ�ͷţ���������պ��ܵ���Q�㲢���ٴη��ؾ���N�㣮��֪�ʵ��һ�λ��������͵�Nʱ����Ϊv1����һ�ε���A��ʱ����Ϊv2��ѡ��N�����ڵ�ˮƽ��Ϊ�������ܵ��������棬�������ٶ�Ϊg��������| A�� | v1=2$\sqrt{gR}$ | |
| B�� | v1��2$\sqrt{gR}$ | |
| C�� | ��N��Q�Ĺ����У�������������ȵĵ���A���Ϸ�����Q��N�Ĺ����У�������������ȵĵ���A���·� | |
| D�� | ��N��Q�Ĺ����У�������������ȵĵ���A���·�����Q��N�Ĺ����У�������������ȵĵ���A���Ϸ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
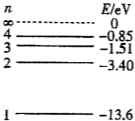 ͼʾΪ��ԭ�ӵ��ܼ�ͼ�����д�������n=4�ܼ�����ԭ������ܼ�ԾǨ������������ӣ�����˵����ȷ���ǣ�������
ͼʾΪ��ԭ�ӵ��ܼ�ͼ�����д�������n=4�ܼ�����ԭ������ܼ�ԾǨ������������ӣ�����˵����ȷ���ǣ�������| A�� | ��Ⱥ��ԭ������ܼ�ԾǨʱ�������ܷ����6�ֲ�ͬƵ�ʵĹ� | |
| B�� | ��Ⱥ��ԭ������ܼ�·Ǩʱ��������������������ֵΪ0.85eV | |
| C�� | ��Ⱥ��ԭ����n=4�ܼ�ԾǨ��n=1�ܼ������Ĺ�Ƶ����� | |
| D�� | ����n=3�ܼ�ԾǨ��n=2�ܼ������Ĺ���ʹij�ֽ����ݳ�����ӣ�����n=2�ܼ�ԾǨ��n=1�ܼ������Ĺ�Ҳһ����ʹ���ֽ����ݳ������ | |
| E�� | ����n=4�ܼ�ԾǨ��n=2�ܼ�����n=3�ܼ�ԾǨ��n=2�ܼ�����n=4�ܼ�ԾǨ��n=3�ܼ������Ĺ�IJ����ֱ�Ϊ��1����2����3�����1=��2+��3 |
�鿴�𰸺ͽ���>>
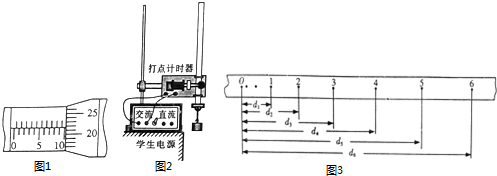
��Ŀ���������� ��Դ�� ���ͣ�ʵ����

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ������ӵ�ƽ���������������ѹǿҲһ������ | |
| B�� | Ҷ���ϵ�С¶�������������Һ��������������� | |
| C�� | Һ���Ĺ�ѧ������ijЩ�������ƣ����и������� | |
| D�� | ��Ϊ�����˶��ļ��ҳ̶����¶��йأ����Բ����˶�Ҳ�������˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ijС������ͼ��ʾ��װ����֤�����غ㶨�ɣ�װ�ù̶���ˮƽ���ϣ�Բ���ι���¶�����ˮƽ������뾶��ͬ��������ˮƽ��Ķ�Ħ��������ͬ��ʵ��ʱ���Ȳ��A��B���������mA��mB������A��δ�Բ���ι����ijһλ���ɾ�ֹ�ͷţ���������ˮƽ���ϻ��о����ƽ��ֵx0��Ȼ�����B�����ڹ���¶�ˮƽ���֣�����A�ӹ����ͬһλ���ɾ�ֹ�ͷţ�����B�������ظ���Σ�
ijС������ͼ��ʾ��װ����֤�����غ㶨�ɣ�װ�ù̶���ˮƽ���ϣ�Բ���ι���¶�����ˮƽ������뾶��ͬ��������ˮƽ��Ķ�Ħ��������ͬ��ʵ��ʱ���Ȳ��A��B���������mA��mB������A��δ�Բ���ι����ijһλ���ɾ�ֹ�ͷţ���������ˮƽ���ϻ��о����ƽ��ֵx0��Ȼ�����B�����ڹ���¶�ˮƽ���֣�����A�ӹ����ͬһλ���ɾ�ֹ�ͷţ�����B�������ظ���Σ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com