
 ��ͼ��ʾ������������ĵ���M��N����������ΪQ���̶��ڹ⻬��Ե��ˮƽ���ϣ����2L��A��O��B��MN�����ϵ����㣬��OΪ�е㣬OA=OB=$\frac{L}{2}$��һ����Ϊm������Ϊq�ĵ����Գ��ٶ�v0��A�������MN������N�˶������˶������е���ܵ���С�㶨���������ã����ٶ�Ϊ��ʱ������ҲΪ�㣬�����˶���O��ʱ������Ϊ�����ܵ�n������B��պ��ٶ�Ϊ�㣬Ȼ�������˶���ֱ�����ֹ����֪����������Ϊk��ȡO������Ϊ�㣮��
��ͼ��ʾ������������ĵ���M��N����������ΪQ���̶��ڹ⻬��Ե��ˮƽ���ϣ����2L��A��O��B��MN�����ϵ����㣬��OΪ�е㣬OA=OB=$\frac{L}{2}$��һ����Ϊm������Ϊq�ĵ����Գ��ٶ�v0��A�������MN������N�˶������˶������е���ܵ���С�㶨���������ã����ٶ�Ϊ��ʱ������ҲΪ�㣬�����˶���O��ʱ������Ϊ�����ܵ�n������B��պ��ٶ�Ϊ�㣬Ȼ�������˶���ֱ�����ֹ����֪����������Ϊk��ȡO������Ϊ�㣮������ ��1��Ӧ�õ��ɵij�ǿ��ʽ�볡�ĵ���ԭ������糡ǿ�ȣ�
��2���ɶ��ܶ������������
��3��Ӧ�ö��ܶ���������ƲȻ����ݵ��Ʋ�Ķ���ʽ������ƣ�
��4��Ӧ�ö��ܶ������·�̣�
��� �⣺��1���ɵ��ɵ糡ǿ�ȹ�ʽ�͵糡����ԭ���ɵã�
E=k$\frac{Q}{��\frac{L}{2}��^{2}}$-k$\frac{Q}{��\frac{3L}{2}��^{2}}$=$\frac{32kQ}{9{L}^{2}}$��
��2���ɶԳ��ԣ�UA=UB����ɴ�A��B�Ĺ����У��糡������Ϊ�㣬�˷���������Ϊ��Wf=fL���ɶ��ܶ�����
-fL=0-$\frac{1}{2}$m$v_0^2$
�ã�f=$\frac{1}{2L}$mv02
��3�����ɴ�A��O��糡������ΪWF���˷���������Ϊ$\frac{1}{2}$Wf��
�ɶ��ܶ�����WF-$\frac{1}{2}$Wf=n$\frac{1}{2}$m$v_0^2$-$\frac{1}{2}$m$v_0^2$
�ã�WF=$\frac{mv_0^2}{4}��2n-1��$
�ɣ�WF=q��UA-UO��
���A=$\frac{W_F}{q}$=$\frac{m{v}_{0}^{2}}{4q}$��2n-1��
��4��������ͣ��O�㣬��ȫ�����е糡������ΪWF=$\frac{mv_0^2}{4}��2n-1��$������ڵ糡���˶�����·��Ϊs������������Ϊ-fs��
�ɶ��ܶ�����WF-fs=0-$\frac{1}{2}$m$v_0^2$
����$\frac{mv_0^2}{4}��2n-1��$-$\frac{1}{2L}$m$v_0^2$s=-$\frac{1}{2}$m$v_0^2$
��ã�s=��n+0.5��L
�𣺣�1��A��ij�ǿ��С$\frac{32kQ}{9{L}^{2}}$��
��2�������Ĵ�С$\frac{1}{2L}$mv02��
��3��A��ĵ���$\frac{m{v}_{0}^{2}}{4q}$��2n-1����
��4������ڵ糡���˶�����·�̣�2n-1��L��
���� ���⿼���˶��ܶ�����Ӧ�ã����������ɵ��˶����̣�Ӧ�ö��ܶ��������ɵij�ǿ��ʽ�볡�ĵ���ԭ��������ȷ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
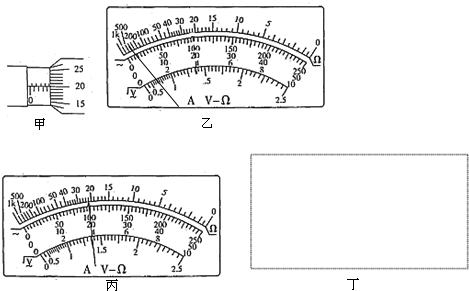
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �ף�m�� | B�� | ǧ�ˣ�kg�� | C�� | �루s�� | D�� | ţ�٣�N�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
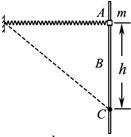 ��ͼ��ʾ�����ʵ���һ�˹̶�����һ����һ����Ϊm�����ڴֲ���ֱ�̶���A����Բ������������ˮƽ�Ҵ���ԭ����Բ����A���ɾ�ֹ��ʼ�»�������B�����ٶ����BΪ��AC��ijһ�㣩������C�����ٶ�Ϊ�㣬AC=h�����Բ����C�����һ��ֱ���ϵ��ٶ�v��ǡ���ܻص�A������ʼ���ڵ������ڣ��������ٶ�Ϊg����Բ����������
��ͼ��ʾ�����ʵ���һ�˹̶�����һ����һ����Ϊm�����ڴֲ���ֱ�̶���A����Բ������������ˮƽ�Ҵ���ԭ����Բ����A���ɾ�ֹ��ʼ�»�������B�����ٶ����BΪ��AC��ijһ�㣩������C�����ٶ�Ϊ�㣬AC=h�����Բ����C�����һ��ֱ���ϵ��ٶ�v��ǡ���ܻص�A������ʼ���ڵ������ڣ��������ٶ�Ϊg����Բ����������| A�� | �»������У����ٶ�һֱ��С | |
| B�� | �»������У��˷�Ħ�������Ĺ�Ϊ$\frac{1}{4}$mv2 | |
| C�� | ��A�»���C�����е��ɵĵ�����������������mgh | |
| D�� | ��C�������ɵĵ�������Ϊ$\frac{1}{4}$mv2-mgh |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
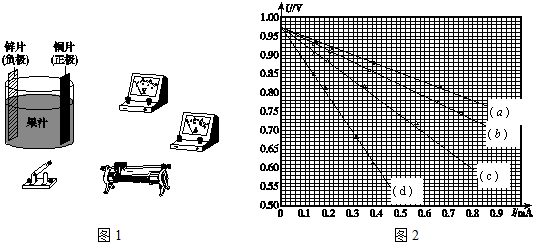
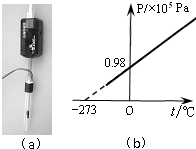 ��DIS�о�һ���������������������ʱѹǿ���¶ȵĹ�ϵ������ʵ��װ����ͼ��a����ʾ���о�����Ϊ�ܱ����Թ��ڵĿ�����ʵ��õ���ͼ��b����ʾ��p-tͼ����ͼ��֪�¶�ÿ����1�棬ѹǿ����359Pa������������ϴ���Թ��ܷ��ʼ�¶Ⱥ�ѹǿ����ͬ�������ٴ�ʵ�飬�õ�ͼ�ߵ�б�ʽ����䣨ѡ���������С�����䡱����
��DIS�о�һ���������������������ʱѹǿ���¶ȵĹ�ϵ������ʵ��װ����ͼ��a����ʾ���о�����Ϊ�ܱ����Թ��ڵĿ�����ʵ��õ���ͼ��b����ʾ��p-tͼ����ͼ��֪�¶�ÿ����1�棬ѹǿ����359Pa������������ϴ���Թ��ܷ��ʼ�¶Ⱥ�ѹǿ����ͬ�������ٴ�ʵ�飬�õ�ͼ�ߵ�б�ʽ����䣨ѡ���������С�����䡱�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
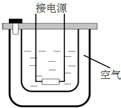 ��ͼΪijʵ�����ĵĽṹʾ��ͼ��������Ͳ�;�����Ͳ������һ��������������壬��Ͳ����ˮ���ڶ�ˮ�������µĹ����У�����յĿ�����������
��ͼΪijʵ�����ĵĽṹʾ��ͼ��������Ͳ�;�����Ͳ������һ��������������壬��Ͳ����ˮ���ڶ�ˮ�������µĹ����У�����յĿ�����������| A�� | ���ܱ��ֲ��� | B�� | ���з����˶����ʶ����� | ||
| C�� | �������ܼ�С | D�� | ����ƽ���������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
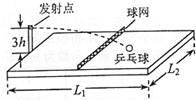 װ��ƹ�����������̨��ͼ��ʾ��ˮƽ̨��ij��Ϳ��ֱ�ΪL1��L2���м������߶�Ϊh���������װ��̨�����Ե���е㣬���Բ�ͬ�������Ҳͬ����ˮƽ����ƹ��������̨��߶�Ϊ3h�����ƿ����������������ٶ�Ϊg����ƹ����ķ�������v��ij��Χ�ڣ�ͨ��ѡ����ʵķ�����ʹƹ�����䵽�����Ҳ�̨���ϣ���v��ȡֵ��Χ�ǣ�������
װ��ƹ�����������̨��ͼ��ʾ��ˮƽ̨��ij��Ϳ��ֱ�ΪL1��L2���м������߶�Ϊh���������װ��̨�����Ե���е㣬���Բ�ͬ�������Ҳͬ����ˮƽ����ƹ��������̨��߶�Ϊ3h�����ƿ����������������ٶ�Ϊg����ƹ����ķ�������v��ij��Χ�ڣ�ͨ��ѡ����ʵķ�����ʹƹ�����䵽�����Ҳ�̨���ϣ���v��ȡֵ��Χ�ǣ�������| A�� | $\frac{{L}_{1}}{4}$$\sqrt{\frac{g}{h}}$��v��$\frac{1}{2}$$\sqrt{\frac{��4{{L}_{1}}^{2}+{{L}_{2}}^{2}��g}{6h}}$ | B�� | $\frac{{L}_{1}}{4}$$\sqrt{\frac{g}{h}}$��v��L1$\sqrt{\frac{g}{6h}}$ | ||
| C�� | $\frac{{L}_{1}}{2}$$\sqrt{\frac{g}{6h}}$��v��$\frac{1}{2}$$\sqrt{\frac{��4{{L}_{1}}^{2}+{{L}_{2}}^{2}��g}{6h}}$ | D�� | $\frac{{L}_{1}}{2}$$\sqrt{\frac{g}{6h}}$��v��L1$\sqrt{\frac{g}{6h}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com