
 得t=2 s
得t=2 s


 mgRcos 53°
mgRcos 53° 。
。


科目:高中物理 来源: 题型:
 滑板运动是一项非常刺激的水上运动,研究表明,在进行滑板运动时,水对滑板的作用力Fx垂直于板面,大小为kv2,其中v为滑板速率(水可视为静止).某次运动中,在水平牵引力作用下,当滑板和水面的夹角θ=37°时如图,滑板做匀速直线运动,相应的k=54kg/m,人和滑板的总质量为108kg,试求(重力加速度g取10m/s2,sin 37°取0.6,忽略空气阻力):
滑板运动是一项非常刺激的水上运动,研究表明,在进行滑板运动时,水对滑板的作用力Fx垂直于板面,大小为kv2,其中v为滑板速率(水可视为静止).某次运动中,在水平牵引力作用下,当滑板和水面的夹角θ=37°时如图,滑板做匀速直线运动,相应的k=54kg/m,人和滑板的总质量为108kg,试求(重力加速度g取10m/s2,sin 37°取0.6,忽略空气阻力):查看答案和解析>>
科目:高中物理 来源: 题型:
 “蹦极”是一项非常刺激的体育运动,某人身系弹性绳自高空P点由静止开始下落,如图所示,a点是弹性绳的原长位置,c是人所到达的最底位置,b是人静止悬挂时平衡的位置,人从 P点落下到最低点c 的过程中( )
“蹦极”是一项非常刺激的体育运动,某人身系弹性绳自高空P点由静止开始下落,如图所示,a点是弹性绳的原长位置,c是人所到达的最底位置,b是人静止悬挂时平衡的位置,人从 P点落下到最低点c 的过程中( )查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,蹦极是一项非常刺激的体育运动,某人身系弹性绳自高空P点由静止开始下落,a点是弹性绳的原长位置,c是所到达的最低位置,b是静止悬挂时平衡的位置,人从P点落下到最低点的过程中( )
如图所示,蹦极是一项非常刺激的体育运动,某人身系弹性绳自高空P点由静止开始下落,a点是弹性绳的原长位置,c是所到达的最低位置,b是静止悬挂时平衡的位置,人从P点落下到最低点的过程中( )查看答案和解析>>
科目:高中物理 来源: 题型:
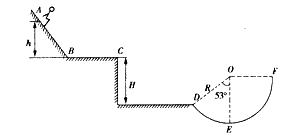
 (2009?泉州二模)高山滑雪是一项很多人喜爱的户外活动.如图所示,滑雪道由一段曲面斜坡和一段水平台面组成,台面离水平地面高为h1,与台面末端点B的水平距离为s的C处有一个高为h2的竖直障碍物CD.某质量为m的运动员,从斜坡上的A点由静止开始沿滑雪道自由下滑,经B点飞出后恰好能从障碍物上端点D越过.若以地面为零重力势能面,运动员在滑雪道滑行过程中损失的机械能为其在A处重力势能的k倍(k<1),重力加速度为g,不计空气阻力.求:
(2009?泉州二模)高山滑雪是一项很多人喜爱的户外活动.如图所示,滑雪道由一段曲面斜坡和一段水平台面组成,台面离水平地面高为h1,与台面末端点B的水平距离为s的C处有一个高为h2的竖直障碍物CD.某质量为m的运动员,从斜坡上的A点由静止开始沿滑雪道自由下滑,经B点飞出后恰好能从障碍物上端点D越过.若以地面为零重力势能面,运动员在滑雪道滑行过程中损失的机械能为其在A处重力势能的k倍(k<1),重力加速度为g,不计空气阻力.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com