
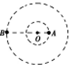
 经长期观测,人们在宇宙中已经发现了“双星系统”.“双星系统”由相距较近的恒星组成,每个恒星的半径远小于两个恒星之间的距离,而且双星系统一般远离其他天体,它们在相互间的万有引力作用下,绕某一点做匀速圆周运动,如图所示为某一双星系统,A星球的质量为m1,B星球的质量为m2,它们中心之间的距离为L,引力常量为G,则下列说法正确的是( )
经长期观测,人们在宇宙中已经发现了“双星系统”.“双星系统”由相距较近的恒星组成,每个恒星的半径远小于两个恒星之间的距离,而且双星系统一般远离其他天体,它们在相互间的万有引力作用下,绕某一点做匀速圆周运动,如图所示为某一双星系统,A星球的质量为m1,B星球的质量为m2,它们中心之间的距离为L,引力常量为G,则下列说法正确的是( )| A. | A星球的轨道半径为R=$\frac{{m}_{1}}{{m}_{1}+{m}_{2}}$L | |
| B. | B星球的轨道半径为r=$\frac{{m}_{2}}{{m}_{1}}$L | |
| C. | 双星运行的周期为T=2πL$\sqrt{\frac{L}{G({m}_{1}+{m}_{2})}}$ | |
| D. | 若近似认为B星球绕A星球中心做圆周运动,则B星球的运行周期为T=2πL$\sqrt{\frac{L}{G{m}_{1}}}$ |
分析 双星靠相互间的万有引力提供向心力,具有相同的角速度.应用牛顿第二定律列方程求解
解答 解:AB、双星靠他们之间的万有引力提供向心力,A星球的轨道半径为R,B星球的轨道半径为r,根据万有引力提供向心力有:
$G\frac{{m}_{1}^{\;}{m}_{2}^{\;}}{{L}_{\;}^{2}}={m}_{1}^{\;}{ω}_{\;}^{2}R={m}_{2}^{\;}{ω}_{\;}^{2}r$
得${m}_{1}^{\;}R={m}_{2}^{\;}r$
且R+r=L
解得:$R=\frac{{m}_{2}^{\;}}{{m}_{1}^{\;}+{m}_{2}^{\;}}L$
$r=\frac{{m}_{1}^{\;}}{{m}_{1}^{\;}+{m}_{2}^{\;}}L$
故A错误,B错误;
C、根据万有引力等于向心力$G\frac{{m}_{1}^{\;}{m}_{2}^{\;}}{{L}_{\;}^{2}}={m}_{1}^{\;}\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}R={m}_{2}^{\;}\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$
得$G{m}_{2}^{\;}{T}_{\;}^{2}=4{π}_{\;}^{2}R{L}_{\;}^{2}$
$G{m}_{1}^{\;}{T}_{\;}^{2}=4{π}_{\;}^{2}r{L}_{\;}^{2}$
得$G({m}_{1}^{\;}+{m}_{2}^{\;}){T}_{\;}^{2}=4{π}_{\;}^{2}(R+r){L}_{\;}^{2}=4{π}_{\;}^{2}{L}_{\;}^{3}$
解得:$T=\sqrt{\frac{4{π}_{\;}^{2}{L}_{\;}^{3}}{G({m}_{1}^{\;}+{m}_{2}^{\;})}}$=$2πL\sqrt{\frac{L}{G({m}_{1}^{\;}+{m}_{2}^{\;})}}$,故C正确;
D、若近似认为B星球绕A星球中心做圆周运动,则根据万有引力提供向心力有:
$G\frac{{m}_{1}^{\;}{m}_{2}^{\;}}{{L}_{\;}^{2}}={m}_{2}^{\;}\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}L$
解得:$T=\sqrt{\frac{4{π}_{\;}^{2}{L}_{\;}^{3}}{G{m}_{1}^{\;}}}$=$2πL\sqrt{\frac{L}{G{m}_{1}^{\;}}}$,故D正确;
故选:CD
点评 解决本题的关键知道双星靠相互间的万有引力提供向心力,具有相同的角速度.以及会用万有引力提供向心力进行求解


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:计算题
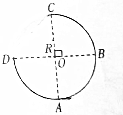 如图所示,半径为R的光滑的四分之三圆弧轨道竖直放置,A、C两点分别为轨道的最低点和最高点,一质量为m的小环套在轨道上,小环以水平向右的初速度从A出发经C点后,恰可撞击到D点.求:
如图所示,半径为R的光滑的四分之三圆弧轨道竖直放置,A、C两点分别为轨道的最低点和最高点,一质量为m的小环套在轨道上,小环以水平向右的初速度从A出发经C点后,恰可撞击到D点.求:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
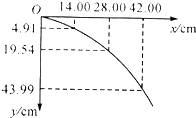 在用斜槽轨道做“研究平抛物体运动”的实验中,简要步骤如下:
在用斜槽轨道做“研究平抛物体运动”的实验中,简要步骤如下:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
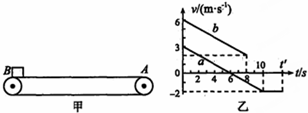 如图甲所示,一个以恒定速率逆时针转动的传送带AB,在其左侧边缘的B点有一个不计大小的滑块,若滑块以初速度v1=3m/s冲上传送带,滑块运动的v-t力象如图乙中实线a所示;若滑块以初速度v2=6m/s冲上传送带,滑块运动的v-t图象如图所乙实线b所示.重力加速度g取10m/s2.求:
如图甲所示,一个以恒定速率逆时针转动的传送带AB,在其左侧边缘的B点有一个不计大小的滑块,若滑块以初速度v1=3m/s冲上传送带,滑块运动的v-t力象如图乙中实线a所示;若滑块以初速度v2=6m/s冲上传送带,滑块运动的v-t图象如图所乙实线b所示.重力加速度g取10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
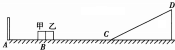 如图所示,高为h的光滑三角形斜劈固定在水平面上,其与水平面平滑对接于C点,D为斜劈的最高点,水平面的左侧A点处有一竖直的弹性挡板,质量均为m的甲、乙两滑块可视为质点,静止在水平面上的B点,已知AB=h,BC=3h,滑块甲与所有接触面的摩擦均可忽略,滑块乙与水平面之间的动摩擦因数为μ=0.5.给滑块甲一水平向左的初速度,经过一系列没有能量损失的碰撞后,滑块乙恰好滑到斜劈的最高点D处,重力加速度用g表示.求:
如图所示,高为h的光滑三角形斜劈固定在水平面上,其与水平面平滑对接于C点,D为斜劈的最高点,水平面的左侧A点处有一竖直的弹性挡板,质量均为m的甲、乙两滑块可视为质点,静止在水平面上的B点,已知AB=h,BC=3h,滑块甲与所有接触面的摩擦均可忽略,滑块乙与水平面之间的动摩擦因数为μ=0.5.给滑块甲一水平向左的初速度,经过一系列没有能量损失的碰撞后,滑块乙恰好滑到斜劈的最高点D处,重力加速度用g表示.求:查看答案和解析>>
科目:高中物理 来源: 题型:实验题
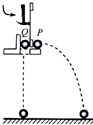 如图所示,在探究平抛运动规律的实验中,用小锤打击弹性金属片,金属片把P球沿水平方向抛出,同时Q球被松开而自由下落,P、Q两球同时开始运动,则:
如图所示,在探究平抛运动规律的实验中,用小锤打击弹性金属片,金属片把P球沿水平方向抛出,同时Q球被松开而自由下落,P、Q两球同时开始运动,则:查看答案和解析>>
科目:高中物理 来源: 题型:实验题
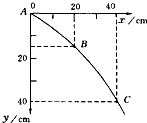 (1)在研究平抛物体的运动的实验中关于造成误差的原因的分析正确的是ACD
(1)在研究平抛物体的运动的实验中关于造成误差的原因的分析正确的是ACD查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,一半径为R=1m的透明介质球,O为球心,光线DC平行于直径AOB射到介质球上的C点,DC与AB的距离H=$\frac{\sqrt{3}}{2}$m;若DC光线进入介质球后第一次到达B并在B处发生全反射.已知光速c=3×108m/s.求:
如图所示,一半径为R=1m的透明介质球,O为球心,光线DC平行于直径AOB射到介质球上的C点,DC与AB的距离H=$\frac{\sqrt{3}}{2}$m;若DC光线进入介质球后第一次到达B并在B处发生全反射.已知光速c=3×108m/s.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com