
| A. | 角速度之比 | B. | 向心加速度之比 | C. | 质量之比 | D. | 所受引力之比 |
分析 根据$ω=\frac{2π}{T}$求角速度之比,根据开普勒第三定律求出轨道半径之比,利用$a={ω}_{\;}^{2}r$求向心加速度之比,根据万有引力提供向心力只能求中心天体质量,根据万有引力得出引力之间的关系.
解答 解:A、根据$ω=\frac{2π}{T}$得,$\frac{{ω}_{1}^{\;}}{{ω}_{2}^{\;}}=\frac{{T}_{2}^{\;}}{{T}_{1}^{\;}}$,所以可以计算角速度之比,故A正确.
B、根据开普勒第三定律$\frac{{r}_{\;}^{3}}{{T}_{\;}^{2}}=k$得$\frac{{r}_{1}^{\;}}{{r}_{2}^{\;}}=\frac{{T}_{1}^{\frac{2}{3}}}{{T}_{2}^{\frac{2}{3}}}$,由$a={ω}_{\;}^{2}r$
得$\frac{{a}_{1}^{\;}}{{a}_{2}^{\;}}=\frac{{T}_{2}^{2}}{{T}_{1}^{2}}\frac{{T}_{1}^{\frac{2}{3}}}{{T}_{2}^{\frac{2}{3}}}=\frac{{T}_{2}^{\frac{4}{3}}}{{T}_{1}^{\frac{4}{3}}}$,所以能求向心加速度之比,故B正确.
C、设“超级地球”的质量为m,恒星质量为M,轨道半径为r,根据万有引力提供向心力,有:
$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$
得:$M=\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{G{T}_{\;}^{2}}$,“超级地球”的质量同时出现在等号两边被约掉,故无法求“超级地球”的质量之比,故C错误.
D、根据万有引力定律$F=G\frac{Mm}{{r}_{\;}^{2}}$,因为无法知道两颗“超级地球”的质量比,所以无法求引力之比,故D错误.
故选:AB
点评 本题考查天体运动,万有引力提供向心力,要注意向心力选择合适公式,同时理解无法求得旋转天体的质量,但中心天体质量可以求得


科目:高中物理 来源: 题型:选择题
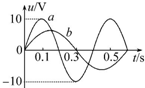 如图所示,图线a是单匝线圈在匀强磁场中匀速转动时产生的正弦交流电的图象,当调整线圈转速后,所产生的正弦交流电的图象如图线b所示.以下关于这两个正弦交流电的说法中正确的是( )
如图所示,图线a是单匝线圈在匀强磁场中匀速转动时产生的正弦交流电的图象,当调整线圈转速后,所产生的正弦交流电的图象如图线b所示.以下关于这两个正弦交流电的说法中正确的是( )| A. | 线圈先后两次转速之比为1:2 | |
| B. | 两次在t=0.6s时线圈平面均与中性面重合 | |
| C. | 交流电b的线圈磁通量变化率的最大值是15Wb/s | |
| D. | 调整转速后,在线圈两端接一电容器,要使电容器不被击穿,电容器的最大承受电压至少为10V |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
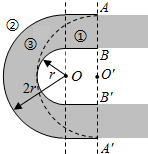 图示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r.一辆质量为m的赛车(视为质点)通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,OO′=r.赛车沿圆弧路线行驶时,路面对轮胎的最大径向(即指向圆心)静摩擦力为Fmax.选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,赛车能达到的速度足够大),则( )
图示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r.一辆质量为m的赛车(视为质点)通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,OO′=r.赛车沿圆弧路线行驶时,路面对轮胎的最大径向(即指向圆心)静摩擦力为Fmax.选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,赛车能达到的速度足够大),则( )| A. | 选择路线①,赛车经过的路程最短 | |
| B. | 选择路线①,赛车的向心加速度最大 | |
| C. | 选择路线③,赛车经过的路程最短 | |
| D. | ①、②、③三条路线的圆弧段,赛车的向心加速度大小相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

 的示数IG和电流表?的示数IA的关系图线如图3所示.由此可知,合金丝接入电路的电阻测量值Rx=4.5Ω(保留两位有效数字).
的示数IG和电流表?的示数IA的关系图线如图3所示.由此可知,合金丝接入电路的电阻测量值Rx=4.5Ω(保留两位有效数字). 的示数IG和电流表?的示数IA也随之增加,图5反映IG-x和IA-x关系的示意图中可能正确的是A.
的示数IG和电流表?的示数IA也随之增加,图5反映IG-x和IA-x关系的示意图中可能正确的是A.
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 质量为2kg的木板B静止在水平面上,可视为质点的物块A从木板的左侧沿木板上表面水平冲上木板,如图甲所示.A和B经过1s达到同一速度之后共同减速直至静止的过程中,A和B的v-t图象如图乙所示,重力加速度g=10m/s2,下面说法中正确的是( )
质量为2kg的木板B静止在水平面上,可视为质点的物块A从木板的左侧沿木板上表面水平冲上木板,如图甲所示.A和B经过1s达到同一速度之后共同减速直至静止的过程中,A和B的v-t图象如图乙所示,重力加速度g=10m/s2,下面说法中正确的是( )| A. | A与B的动摩擦因数μ1=0.2 | B. | B与地面间的动摩擦因数μ2=0.2 | ||
| C. | A物块的质量mA=6kg | D. | A、B间因摩擦产生的热量为48J |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com