
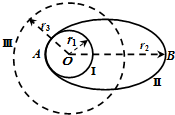
 地球质量为M,半径为R,自转周期为T0,取无穷远处的引力势能为零.质量为m的卫星在绕地球无动力飞行时,它和地球组成的系统机械能守恒,它们之间引力势能的表达式是Ep=-$\frac{GMm}{r}$,其中r是卫星与地心间的距离.现欲将质量为m的卫星从近地圆轨道Ⅰ发射到椭圆轨道Ⅱ上去,轨道Ⅱ的近地点A和远地点B距地心分别为r1=R,r2=3R.若卫星在轨道Ⅱ上的机械能和在r3=2R的圆周轨道Ⅲ上的机械能相同,则( )
地球质量为M,半径为R,自转周期为T0,取无穷远处的引力势能为零.质量为m的卫星在绕地球无动力飞行时,它和地球组成的系统机械能守恒,它们之间引力势能的表达式是Ep=-$\frac{GMm}{r}$,其中r是卫星与地心间的距离.现欲将质量为m的卫星从近地圆轨道Ⅰ发射到椭圆轨道Ⅱ上去,轨道Ⅱ的近地点A和远地点B距地心分别为r1=R,r2=3R.若卫星在轨道Ⅱ上的机械能和在r3=2R的圆周轨道Ⅲ上的机械能相同,则( )| A. | 卫星在近地圆轨道Ⅰ上运行的周期与地球自转周期相同 | |
| B. | 从轨道Ⅰ发射到轨道Ⅱ需要在近地的A点一次性给它提供能量$\frac{GMm}{4R}$ | |
| C. | 卫星在椭圆轨道上的周期为T0$\sqrt{(\frac{{r}_{2}+R}{R})^{3}}$ | |
| D. | 卫星在椭圆轨道Ⅱ上自由运行时,它在B点的机械能大于在A点的机械能 |
分析 根据开普勒第三定律比较卫星在近地圆轨道Ⅰ上运行的周期与地球同步卫星周期的关系,即得到与地球自转周期关系.根据能量守恒定律求卫星变轨需要提供的能量.由开普勒第三定律求卫星在椭圆轨道上的周期.卫星在椭圆轨道上运动时机械能是守恒的.
解答 解:A、根据开普勒第三定律可知,卫星在近地圆轨道Ⅰ上运行的周期小于地球同步卫星周期,即小于地球自转周期.故A错误.
B、设从轨道Ⅰ发射到轨道Ⅱ需要在近地的A点一次性给它提供能量为E.卫星在轨道Ⅰ和轨道Ⅲ上的速率分别为v1和v3.
则v1=$\sqrt{\frac{GM}{R}}$,v3=$\sqrt{\frac{GM}{2R}}$
据题知,卫星在轨道Ⅱ上的机械能和在r3=2R的圆周轨道Ⅲ上的机械能相同,根据能量守恒定律得:
-$\frac{GMm}{R}$+$\frac{1}{2}m{v}_{1}^{2}$+E=$\frac{1}{2}m{v}_{3}^{2}$+(-$\frac{GMm}{2R}$)
联立解得 E=$\frac{GMm}{4R}$.故B正确.
C、设卫星在椭圆轨道上的周期为T,而地球同步卫星的轨道半径为r.根据开普勒第三定律得:
$\frac{(\frac{{r}_{1}+{r}_{2}}{2})^{3}}{{T}^{2}}$=$\frac{{r}^{3}}{{T}_{0}^{2}}$
即:r1=R,r2=3R,而r>R
解得 T=T0$\sqrt{(\frac{{r}_{2}+R}{2r})^{3}}$,2r≠R,故C错误.
D、卫星在椭圆轨道Ⅱ上自由运行时,只有万有引力对它做功,其机械能守恒,则它在B点的机械能等于在A点的机械能.故D错误.
故选:B
点评 本题是信息给予题,首先要读懂题意,知道引力势能的表达式是Ep=-$\frac{GMm}{r}$,要知道r的准确含义:r是卫星与地心间的距离.要注意只有卫星做匀速圆周运动,才能根据万有引力等于向心力列式.对于椭圆运动,应根据开普勒定律研究卫星的运动规律.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中物理 来源: 题型:多选题
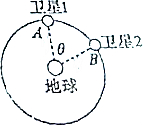 2015年3月30日,我国成功发射一颗北斗导航卫星.这是我国发射的第17颗北斗导航卫星,这次成功发射,标志着北斗导航系统由区域运行开始向全球组网.如图所示,北斗导航系统中的两颗地球同步卫星1、2轨道半径均为r,某时刻分别位于轨道上的A、B两个位置,若卫星均沿顺时针方向运行,地球表面的重力加速为g,地球半径为R,不计卫星间的相互作用力,下列判断正确的是( )
2015年3月30日,我国成功发射一颗北斗导航卫星.这是我国发射的第17颗北斗导航卫星,这次成功发射,标志着北斗导航系统由区域运行开始向全球组网.如图所示,北斗导航系统中的两颗地球同步卫星1、2轨道半径均为r,某时刻分别位于轨道上的A、B两个位置,若卫星均沿顺时针方向运行,地球表面的重力加速为g,地球半径为R,不计卫星间的相互作用力,下列判断正确的是( )| A. | 卫星1向后喷气就一定能够追上卫星2 | |
| B. | 两卫星及其各部分均处于完全失重状态 | |
| C. | 这两颗卫星的线速度大小相等,均为$\sqrt{\frac{GM}{r}}$ | |
| D. | 卫星1由A位置石动到B位置所需的时间是$\frac{θ}{R}$$\sqrt{\frac{{r}^{3}}{g}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 如图为一个测温装置,图中C为测温泡,装入水银的U形管B管开口向上,A管通过细玻璃管与测温泡C相通,U形管的下端通过软管相连.测温时,调节B管的高度,使A管中的液面保持在a处,此时根据U形管A、B两管水银面的高度差就能知道测温泡所处环境的温度.假设该测温装置在制定刻度时的大气压为76cmHg,该温度计的0℃和30℃刻度线间的距离正好是30cm.
如图为一个测温装置,图中C为测温泡,装入水银的U形管B管开口向上,A管通过细玻璃管与测温泡C相通,U形管的下端通过软管相连.测温时,调节B管的高度,使A管中的液面保持在a处,此时根据U形管A、B两管水银面的高度差就能知道测温泡所处环境的温度.假设该测温装置在制定刻度时的大气压为76cmHg,该温度计的0℃和30℃刻度线间的距离正好是30cm.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 5 6 | B. | 8 4 | C. | 8 6 | D. | 6 6 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 明矾、云母、松香、味精都属于晶体 | |
| B. | 在熔化过程中,晶体要吸收热量,但温度保持不变,内能也保持不变 | |
| C. | 在合适的条件下,某些晶体可以转化为非晶体,某些非晶体也可以转化为晶体 | |
| D. | 由于多晶体是许多单晶体杂乱无章地组合而成的,所以多晶体是各向异性的 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
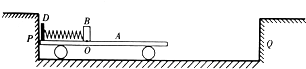
 如图所示,某同学为验证动能定理设计了如图所示的实验,橡皮筋固定在桌子的右端,一质量为m的小车固定在橡皮筋上,小车在O位置时橡皮筋恰好处于原长,完全相同的橡皮筋条数可以更换,A位置为光电门,小车上挡板的宽度为D,OA间的距离为L,砝码与托盘的总质量为M,小车与桌面间的摩擦忽略不计.
如图所示,某同学为验证动能定理设计了如图所示的实验,橡皮筋固定在桌子的右端,一质量为m的小车固定在橡皮筋上,小车在O位置时橡皮筋恰好处于原长,完全相同的橡皮筋条数可以更换,A位置为光电门,小车上挡板的宽度为D,OA间的距离为L,砝码与托盘的总质量为M,小车与桌面间的摩擦忽略不计.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,气垫导轨的滑块上安装了宽度为d的遮光板,做加速运动的滑块先后通过两个光电门,数字毫秒计记录了遮光板通过第一个光电门的时间为t1,通过第二个光电门的时间为t2,遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为△t,下列测量结果中最接近真实值的是( )
如图所示,气垫导轨的滑块上安装了宽度为d的遮光板,做加速运动的滑块先后通过两个光电门,数字毫秒计记录了遮光板通过第一个光电门的时间为t1,通过第二个光电门的时间为t2,遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为△t,下列测量结果中最接近真实值的是( )| A. | 滑块运动的加速度为$\frac{{d({t_1}-{t_2})}}{{{t_1}{t_2}(△t)}}$ | |
| B. | 滑块运动的加速度为$\frac{{2d({t_1}-{t_2})}}{{{t_1}{t_2}[{2(△t)+{t_2}-{t_1}}]}}$ | |
| C. | 遮光板中点通过第一个光电门的速度为$\frac{d}{t_1}$ | |
| D. | 遮光板前沿通过第一个光电门的速度为$\frac{d}{t_1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com