
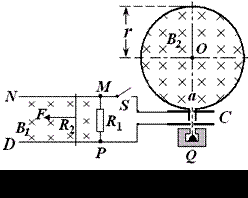
如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距l = 0.2m,电阻R1 = 0.4Ω,导轨上静止放置一质量m = 0.1kg、电阻R2 = 0.1Ω的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度B1 = 0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末杆的速度为2.5m/s,求:
(1)5s末时电阻R上消耗的电功率;
(2)5s末时外力F的功率.
(3)若杆最终以8 m/s的速度作匀速运动, 此时闭合电键S,![]() 射线源Q释放的
射线源Q释放的![]() 粒子经加速电场C加速后从a孔对着圆心O进入半径r =
粒子经加速电场C加速后从a孔对着圆心O进入半径r = ![]() m的固定圆筒中(筒壁上的小孔a只能容一个粒子通过),圆筒内有垂直水平面向下的磁感应强度为B2的匀强磁场。
m的固定圆筒中(筒壁上的小孔a只能容一个粒子通过),圆筒内有垂直水平面向下的磁感应强度为B2的匀强磁场。![]() 粒子每次与筒壁发生碰撞均无电荷迁移,也无机械能损失,粒子与圆筒壁碰撞5次后恰又从a孔背离圆心射出,忽略
粒子每次与筒壁发生碰撞均无电荷迁移,也无机械能损失,粒子与圆筒壁碰撞5次后恰又从a孔背离圆心射出,忽略![]() 粒子进入加速电场的初速度,若
粒子进入加速电场的初速度,若![]() 粒子质量
粒子质量![]() = 6.6×10-27 kg , 电量
= 6.6×10-27 kg , 电量![]() = 3.2×10-19 C, 则磁感应强度B2 多大?若不计碰撞时间,粒子在圆筒内运动的总时间多大?
= 3.2×10-19 C, 则磁感应强度B2 多大?若不计碰撞时间,粒子在圆筒内运动的总时间多大?
(1) 0.1 W (2) 0.25W (3) ![]() 1.57×10 -2 s
1.57×10 -2 s
(1)5s末杆产生的电动势 E =B l v = 0.5 ×0.2 ×2.5 V = 0.25 V
![]() A = 0.5 A
A = 0.5 A
电阻上消耗的电功率 PR = I 2 R1 = 0.1 W (4分)
(2)金属棒的加速度![]()
由牛顿定律 F- F安 = ma
杆受的安培力 F安 = B I l
外力F的功率 P =Fv
由以上各式得 P = ( B I l + ma ) v = 0.25W(6分)
(3)此时回路电流强度为 ![]() A = 1.6A
A = 1.6A
加速电场的电压为 U = IR 1= 1.6×0.4 V = 0.64 V
根据动能定理:![]() =
= ![]()
![]() 粒子从C孔进入磁场的速度v =
粒子从C孔进入磁场的速度v =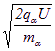 =
=![]() m/s ≈8.0×103 m/s (4分)
m/s ≈8.0×103 m/s (4分)
由题意知:![]() 粒子与圆筒壁碰撞5次后从a孔离开磁场, 由几何关系求得∠d O b = 60°
粒子与圆筒壁碰撞5次后从a孔离开磁场, 由几何关系求得∠d O b = 60°
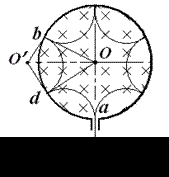 轨迹半径R' =
轨迹半径R' =![]() = 1.0 m
= 1.0 m
又: ![]()
故: ![]() =
= ![]() T =1.65×10-5 T
T =1.65×10-5 T
又:∠d O'b = ![]() , 粒子作圆周运动转过的圆心角为
, 粒子作圆周运动转过的圆心角为![]()
根据 ![]() 及 v =
及 v = ![]()
得 T = ![]() =
= ![]() s = 7.85×10-3 s
s = 7.85×10-3 s
粒子在圆筒内运动的总时间 t = 2T = 2×7.85×10-3 s = 1.57×10 -2 s (7分)


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中物理 来源: 题型:
 如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距L=0.2m,电阻R=0.4Ω,导轨上静止放置一质量为m=0.1kg、电阻r=0.1Ω的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度B=0.5T的匀强磁场中,磁场方向竖直向下,现用一个外力F沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末理想电压表的读数为0.2V.求
如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距L=0.2m,电阻R=0.4Ω,导轨上静止放置一质量为m=0.1kg、电阻r=0.1Ω的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度B=0.5T的匀强磁场中,磁场方向竖直向下,现用一个外力F沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末理想电压表的读数为0.2V.求查看答案和解析>>
科目:高中物理 来源: 题型:
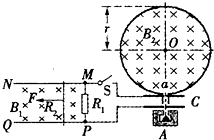 如图所示,光滑且足够长的平行导轨MN和PQ固定在同一水平面上,两导轨间距L=0.2m,电阻R1=0.4Ω,导轨上静止放置一质量m=0.1kg,电阻R2=0.1Ω的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度B1=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆,使之由静止开始做匀加速运动并开始计时,若5s末杆的速度为2.5m/s,求:
如图所示,光滑且足够长的平行导轨MN和PQ固定在同一水平面上,两导轨间距L=0.2m,电阻R1=0.4Ω,导轨上静止放置一质量m=0.1kg,电阻R2=0.1Ω的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度B1=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆,使之由静止开始做匀加速运动并开始计时,若5s末杆的速度为2.5m/s,求:| 3 |
| 6.4 |
| 6.6 |
查看答案和解析>>
科目:高中物理 来源: 题型:
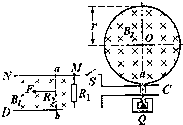 如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距离L=0.2m,电阻R1=0.4Ω,导轨上静止放置一质量m=0.1kg,电阻R2=0.1Ω的金属杆ab,导轨电阻忽略不计,整个装置处在磁感应强度B1=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆ab,使之由静止开始运动,最终以8m/s的速度做匀速直线运动.若此时闭合开关S,释放的α粒子经加速电场C加速从a孔对着圆心O进入半径r=
如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距离L=0.2m,电阻R1=0.4Ω,导轨上静止放置一质量m=0.1kg,电阻R2=0.1Ω的金属杆ab,导轨电阻忽略不计,整个装置处在磁感应强度B1=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆ab,使之由静止开始运动,最终以8m/s的速度做匀速直线运动.若此时闭合开关S,释放的α粒子经加速电场C加速从a孔对着圆心O进入半径r=| 3 |
294 63 |
295 56 |
256 60 |
258 58 |
查看答案和解析>>
科目:高中物理 来源: 题型:
如图所示,光滑且足够长的平行金属导轨![]() 和
和![]() 固定在同一水平面上,两导轨间距,电阻
固定在同一水平面上,两导轨间距,电阻![]() ,导轨上静止放置一质量
,导轨上静止放置一质量![]() 、电阻
、电阻![]() 的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度
的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度![]() 的匀强磁场中,磁场的方向竖直向下,现用一外力
的匀强磁场中,磁场的方向竖直向下,现用一外力![]() 沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末理想电压表的读数为0.2V.求:
沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末理想电压表的读数为0.2V.求:
(1)5s末时电阻![]() 上消耗的电功率;
上消耗的电功率;
(2)金属杆在5s末的运动速率;
(3)5s末时外力![]() 的功率.
的功率.

查看答案和解析>>
科目:高中物理 来源: 题型:
如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距离L=0.2m,电阻R1=0.4![]() ,导轨上静止放置一质量m=0.1kg,电阻R2=0.1
,导轨上静止放置一质量m=0.1kg,电阻R2=0.1![]() 的金属杆ab,导轨电阻忽略不计,整个装置处在磁感应强度B1=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆ab,使之由静止开始运动,最终以8m/s的速度做匀速直线运动。若此时闭合开关S,释放的
的金属杆ab,导轨电阻忽略不计,整个装置处在磁感应强度B1=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆ab,使之由静止开始运动,最终以8m/s的速度做匀速直线运动。若此时闭合开关S,释放的![]() 粒子经加速电场C加速从a孔对着圆心O进入半径r=
粒子经加速电场C加速从a孔对着圆心O进入半径r=![]() 的固定圆筒中(筒壁上的小孔a只能容一个粒子通过),圆筒内有垂直水平面向下的磁感应强度为B2的匀强磁场,
的固定圆筒中(筒壁上的小孔a只能容一个粒子通过),圆筒内有垂直水平面向下的磁感应强度为B2的匀强磁场,![]() 粒子每次与筒壁发生碰撞均无电荷迁移,也无机械能损失。(
粒子每次与筒壁发生碰撞均无电荷迁移,也无机械能损失。(![]() 粒子质量m≈6.4×10-23kg,电荷量q=3.2×10-19C)。求:
粒子质量m≈6.4×10-23kg,电荷量q=3.2×10-19C)。求:

(1)ab杆做匀速直线运动过程中,外力F的功率;
(2)![]() 射线源Q是钍核
射线源Q是钍核![]() 发生衰变生成镭核
发生衰变生成镭核
![]() 并粒出一个
并粒出一个![]() 粒子,完成下列钍核的衰变方程
粒子,完成下列钍核的衰变方程![]() ;
;
(3)若![]() 粒子与圆筒壁碰撞5次后恰又从a孔背离圆心射出,忽略
粒子与圆筒壁碰撞5次后恰又从a孔背离圆心射出,忽略![]() 粒子进入加速电场的初速度,求磁感应强度B2。
粒子进入加速电场的初速度,求磁感应强度B2。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com