
 据悉,神舟十号飞船计划于2013年6月上旬发射,它标志着我国载人航天工程技术日臻成熟.现假设飞船正常飞行地圆轨道半径为R,若要返回地面,可在轨道上某点A处,将速率减小到适当值,使飞船沿着以地心为焦点的椭圆轨道运动(在椭圆轨道上只受重力作用),椭圆与地球表面在B点相切(即着地点),假设着陆时不用减速,已知地球半径为R0,地表处的重力加速度为g.求:
据悉,神舟十号飞船计划于2013年6月上旬发射,它标志着我国载人航天工程技术日臻成熟.现假设飞船正常飞行地圆轨道半径为R,若要返回地面,可在轨道上某点A处,将速率减小到适当值,使飞船沿着以地心为焦点的椭圆轨道运动(在椭圆轨道上只受重力作用),椭圆与地球表面在B点相切(即着地点),假设着陆时不用减速,已知地球半径为R0,地表处的重力加速度为g.求:分析 (1)飞船返回时是沿地心为焦点的椭圆轨道运行,由开普勒第三定律可求飞船的返回时间;(2)根据万有引力定律和开普勒第二定律(公式表达为v1r1=v2r2)可求飞船在A点应该减小到的速率.
解答 解:(1)飞船返回时间为运行周期T′的一半,而半长轴为$\frac{1}{2}(R+{R}_{0})$,
由开普勒定律可得:$\frac{{R}^{2}}{{T}^{3}}=\frac{{(\frac{R+{R}_{0}}{2})}^{2}}{T{′}^{3}}$,
所以飞船由A到B经历的时间$t=\frac{1}{2}T′$.
以上各式联立得,$t=\frac{\sqrt{2}}{8}{(1+\frac{{R}_{0}}{R})}^{\frac{3}{2}}T$.
(2)飞船着陆时,有:$\frac{{m{v}_{B}}^{2}}{{R}_{0}}=mg$
根据开普勒第二定律知,vAR=vBR0
两式联立得,飞船在A点应该减小到的速率:${v}_{A}=\frac{{R}_{0}}{R}\sqrt{{gR}_{0}}$.
答:(1)飞船由A到B经历的时间为$\frac{\sqrt{2}}{8}{(1+\frac{{R}_{0}}{R})}^{\frac{3}{2}}T$;
(2)飞船在A点应该减小到的速率为$\frac{{R}_{0}}{R}\sqrt{{gR}_{0}}$.
点评 开普勒定律虽是对太阳行星而言,同样也适用于地球卫星系统,绕同一天体运行的星体可用开普勒第三定律研究半径和周期的关系.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中物理 来源: 题型:多选题
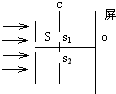
| A. | 去掉单缝S,屏上无干涉条纹 | |
| B. | 去掉双缝C,屏上将无任何条纹 | |
| C. | 用不同颜色的透明玻璃分别遮住S1、S2,屏上将无任何干涉条纹 | |
| D. | 无论普通光源频率如何变化,屏中央O处始终为亮条纹 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,在水平向右的匀强电场E中,虚线是某带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上两点.若带电粒子在运动中只受电场力作用,则由此图可判断出( )
如图所示,在水平向右的匀强电场E中,虚线是某带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上两点.若带电粒子在运动中只受电场力作用,则由此图可判断出( )| A. | 带电粒子带负电 | B. | 带电粒子带正电 | ||
| C. | 带电粒子所受电场力向左 | D. | 带电粒子做匀变速运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,一小木块在沿倾角为370的斜面上受沿斜面向上的恒定外力F作用,从A点由静止开始做匀加速运动,前进4m到达B点,速度达到8m/s,木块与斜面间的动摩擦因数μ=0.5,木块质量m=1kg.(g=10m/s2,Sin37°=0.6,cos37°=0.8 ).求:
如图所示,一小木块在沿倾角为370的斜面上受沿斜面向上的恒定外力F作用,从A点由静止开始做匀加速运动,前进4m到达B点,速度达到8m/s,木块与斜面间的动摩擦因数μ=0.5,木块质量m=1kg.(g=10m/s2,Sin37°=0.6,cos37°=0.8 ).求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
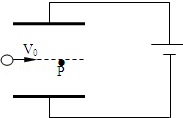 如图所示,水平放置的平行板电容器两板间距为d,板长为L,接在电压为U的直流电源上,有一质量为m的带电液滴以初速度v0从板间的正中点水平射入,恰好做匀速直线运动,当它运动到P处时迅速将下板向上提起$\frac{d}{6}$,液滴刚好从金属板右边缘飞出,求:
如图所示,水平放置的平行板电容器两板间距为d,板长为L,接在电压为U的直流电源上,有一质量为m的带电液滴以初速度v0从板间的正中点水平射入,恰好做匀速直线运动,当它运动到P处时迅速将下板向上提起$\frac{d}{6}$,液滴刚好从金属板右边缘飞出,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 如图所示,框架面积为S,框架平面与磁感应强度为B的匀强磁场方向垂直,则穿过线框平面的磁通量为BS,若使框架绕轴OO′转过60°角,则穿过线框平面的磁通量为0.5BS;若从初始位置转过90°角,则穿过线框平面的磁通量为0;若从初始位置转过180°角,则穿过线框平面的磁通量的变化量为-2BS.
如图所示,框架面积为S,框架平面与磁感应强度为B的匀强磁场方向垂直,则穿过线框平面的磁通量为BS,若使框架绕轴OO′转过60°角,则穿过线框平面的磁通量为0.5BS;若从初始位置转过90°角,则穿过线框平面的磁通量为0;若从初始位置转过180°角,则穿过线框平面的磁通量的变化量为-2BS.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
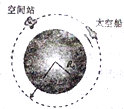 2015年9月18日消息,美国“天龙号”载人太空船2017年前往国际空间站.假设太空船与国际空间站都位于离地球表面为H的圆形轨道上,国际空间站在太空船前方,如图所示,已知地球半径为R0,地球表面重力加速度为g,第一宇宙速度为v,求:
2015年9月18日消息,美国“天龙号”载人太空船2017年前往国际空间站.假设太空船与国际空间站都位于离地球表面为H的圆形轨道上,国际空间站在太空船前方,如图所示,已知地球半径为R0,地球表面重力加速度为g,第一宇宙速度为v,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com