

| F |
| 2 |
| F |
| 2 |
| 12N |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| v2′-v2 |
| -μg |
| 8-12 |
| -0.2×10 |
| △v |
| a |
| v-v1′ |
| μg |
| 4-2 |
| 0.2×10 |
| v1′+v |
| 2 |
| 2+4 |
| 2 |


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中物理 来源: 题型:
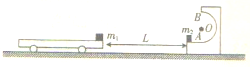 如图所示,一足够长的平板车静止在水平地面上,右端放有质量m1=1.0kg的小物块a,物块与车的上表面间的动摩擦因数μ=0.5物体与车之间的最大静摩擦力等于滑动摩擦力,距离车的右端L=11.5m处有一光滑平台,平台与一固定在地面上的半径R=0.9m的光滑半圆形轨道底端相切,半圆形轨道直径AOB竖直,车的上表面和平台的高度相同.平台的左端有一静止的质量为m2=1.0kg的小物块b.某时刻车在外力作用下由静止开始以a=5.75m/s2的加速度向右做匀加速运动,车碰到平台后立即跟平台粘在一起,两小物块的碰撞没有能量损失(g=10.0m/s2)
如图所示,一足够长的平板车静止在水平地面上,右端放有质量m1=1.0kg的小物块a,物块与车的上表面间的动摩擦因数μ=0.5物体与车之间的最大静摩擦力等于滑动摩擦力,距离车的右端L=11.5m处有一光滑平台,平台与一固定在地面上的半径R=0.9m的光滑半圆形轨道底端相切,半圆形轨道直径AOB竖直,车的上表面和平台的高度相同.平台的左端有一静止的质量为m2=1.0kg的小物块b.某时刻车在外力作用下由静止开始以a=5.75m/s2的加速度向右做匀加速运动,车碰到平台后立即跟平台粘在一起,两小物块的碰撞没有能量损失(g=10.0m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:
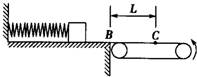 如图所示,质量为m=1kg的滑块,放在光滑的水平平台上,平台的右端B与足够长的水平传送带相接,皮带轮的半径为R=o.5m,且以角速度ω=12rad/s逆时针转动(传送带不打滑),先将滑块缓慢向左压缩固定在平台上的轻弹簧,然后突然释放,当滑块滑到传送带上距B端L=15m的C点时,与传送带速度大小相等,滑块与传送带之间的动摩擦因数μ=0.15.(g=10m/s2)求:
如图所示,质量为m=1kg的滑块,放在光滑的水平平台上,平台的右端B与足够长的水平传送带相接,皮带轮的半径为R=o.5m,且以角速度ω=12rad/s逆时针转动(传送带不打滑),先将滑块缓慢向左压缩固定在平台上的轻弹簧,然后突然释放,当滑块滑到传送带上距B端L=15m的C点时,与传送带速度大小相等,滑块与传送带之间的动摩擦因数μ=0.15.(g=10m/s2)求:查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源:2013-2014学年浙江省高三上学期期中考试物理试卷(解析版) 题型:计算题
如图所示,质量为m=1 kg的滑块,放在光滑的水平平台上,平台的右端B与足够长的水平传送带相接,皮带轮的半径为R=0.5m,且以角速度ω=12 rad/s逆时针转动(传送带不打滑),先将滑块缓慢向左压缩固定在平台上的轻弹簧,然后突然释放,当滑块滑到传送带上距B端L=15m的C点时,与传送带速度大小相等,滑块与传送带之间的动摩擦因数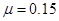 。(g=10 m/s2)求:
。(g=10 m/s2)求:
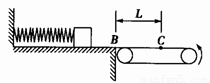
(1)释放滑块前弹簧具有的弹性势能;
(2)滑块从B到C所用的时间;
(3) 滑块从B到C系统因摩擦增加的内能。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com