
| A. | 四颗星围绕正方形对角线的交点做匀速圆周运动 | |
| B. | 四颗星的线速度均为$\sqrt{\frac{Gm}{a}(2+\frac{\sqrt{2}}{4})}$ | |
| C. | 四颗星表面的重力加速度均为$\frac{Gm}{{R}^{2}}$ | |
| D. | 四颗星的周期均为2πa$\sqrt{\frac{2a}{(4+\sqrt{2})Gm}}$ |
分析 在四颗星组成的四星系统中,其中任意一颗星受到其它三颗星对它的合力提供圆周运动的向心力,根据合力提供向心力,求出星体匀速圆周运动的线速度和周期.
根据万有引力等于重力,求出星体表面的重力加速度.
解答 解:A、星体在其他三个星体的万有引力作用下,合力方向指向对角线的交点,围绕正方形对角线的交点做匀速圆周运动,故A正确.
B、星体在其他三个星体的万有引力作用下围绕正方形对角线的交点做匀速圆周运动,由万有引力定律和向心力公式得:$G\frac{{m}_{\;}^{2}}{(\sqrt{2}a)_{\;}^{2}}+\sqrt{2}\frac{G{m}_{\;}^{2}}{{a}_{\;}^{2}}=m\frac{{v}_{\;}^{2}}{\frac{\sqrt{2}a}{2}}$
解得$v=\sqrt{\frac{Gm}{a}(1+\frac{\sqrt{2}}{4})}$,故B错误;
C、根据万有引力等于重力,$\frac{Gmm′}{{R}_{\;}^{2}}=m′g$,得$g=\frac{Gm}{{R}_{\;}^{2}}$,故C正确;
D、星体在其他三个星体的万有引力作用下围绕正方形对角线的交点做匀速圆周运动,由万有引力定律和向心力公式得:$T=\frac{2π×\frac{\sqrt{2}a}{2}}{v}=\frac{\sqrt{2}πa}{\sqrt{\frac{Gm}{a}(1+\frac{\sqrt{2}}{4})}}$=$2π\sqrt{\frac{2{a}_{\;}^{3}}{(4+\sqrt{2})Gm}}$=$2πa\sqrt{\frac{2a}{(4+\sqrt{2})Gm}}$,故D正确;
故选:ACD
点评 解决本题的关键掌握万有引力等于重力,以及知道在四颗星组成的四星系统中,其中任意一颗星受到其它三颗星对它的合力提供圆周运动的向心力.


科目:高中物理 来源: 题型:选择题
 平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示,若平抛运动的时间大于2t1,则下列说法中正确的是( )
平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示,若平抛运动的时间大于2t1,则下列说法中正确的是( )| A. | 图线2表示水平分运动的v-t图线 | |
| B. | t1时刻的速度方向与初速度方向夹角为30° | |
| C. | t1时刻的位移方向与初速度方向夹角的正切为1 | |
| D. | 2t1时刻的位移方向与初速度方向夹角为45° |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
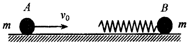 如图所示,光滑水平面上,质量为m的小球B连接着轻质弹簧,处于静止状态;质量也为m的小球A以某一速度向右匀速运动,已知碰撞过程中总机械能守恒,两球距离最近时弹簧的弹性势能为EP,则碰前A球的速度为2$\sqrt{\frac{{E}_{p}}{m}}$.
如图所示,光滑水平面上,质量为m的小球B连接着轻质弹簧,处于静止状态;质量也为m的小球A以某一速度向右匀速运动,已知碰撞过程中总机械能守恒,两球距离最近时弹簧的弹性势能为EP,则碰前A球的速度为2$\sqrt{\frac{{E}_{p}}{m}}$.查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
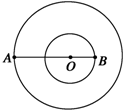 如图所示,双星系统中的星球A、B都可视为质点,A、B绕两者连线上的O点做匀速圆周运动,A、B之间距离不变,观测到A的速率为v、运行周期为T,二者质量分别为m1、m2.则B的周期为T;B的速率为$\frac{{m}_{1}^{\;}v}{{m}_{2}^{\;}}$(用题中物理量字母表示)
如图所示,双星系统中的星球A、B都可视为质点,A、B绕两者连线上的O点做匀速圆周运动,A、B之间距离不变,观测到A的速率为v、运行周期为T,二者质量分别为m1、m2.则B的周期为T;B的速率为$\frac{{m}_{1}^{\;}v}{{m}_{2}^{\;}}$(用题中物理量字母表示)查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 风洞飞行表演是一种高科技的惊险的娱乐节目.在某次表演中,假设风洞内向上的总风量和风速保持不变.质量为m的表演者通过调整身姿,可改变所受的向上的风力大小,以获得不同的运动效果.假设人体受风力大小与正对面积成正比,已知水平横躺时受风力面积最大,且人体站立时受风力面积为水平横躺时受风力面积的$\frac{1}{8}$,风洞内人体可上下移动的空间总高度AC=H.开始时,若人体与竖直方向成一定角度倾斜时,受风力有效面积是最大值的一半,恰好使表演者在最高点A点处于静止状态;后来,表演者从A点开始,先以向下的最大加速度匀加速下落,经过某处B点后,再以向上的最大加速度匀减速下落,刚好能在最低点C处减速为零,试求:
风洞飞行表演是一种高科技的惊险的娱乐节目.在某次表演中,假设风洞内向上的总风量和风速保持不变.质量为m的表演者通过调整身姿,可改变所受的向上的风力大小,以获得不同的运动效果.假设人体受风力大小与正对面积成正比,已知水平横躺时受风力面积最大,且人体站立时受风力面积为水平横躺时受风力面积的$\frac{1}{8}$,风洞内人体可上下移动的空间总高度AC=H.开始时,若人体与竖直方向成一定角度倾斜时,受风力有效面积是最大值的一半,恰好使表演者在最高点A点处于静止状态;后来,表演者从A点开始,先以向下的最大加速度匀加速下落,经过某处B点后,再以向上的最大加速度匀减速下落,刚好能在最低点C处减速为零,试求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| 星球 | 金星 | 地球 | 火星 |
| 公转半径 | 1.0×108km | 1.5×108km | 2.25×108km |
| 自转周期 | 243日 | 23时56分 | 24时37分 |
| 表面温度 | 480℃ | 15℃ | -100℃~0℃ |
| A. | 金星公转的线速度最小,火星公转的线速度最大 | |
| B. | 金星公转的向心加速度大于地球公转的向心加速度 | |
| C. | 金星的公转周期一定比地球的公转周期小 | |
| D. | 金星的公转角速度一定比地球的大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 若A、B、C三物体随转台一起转动而未发生滑动,A、C的向心加速度比B大 | |
| B. | 若A、B、C三物体随转台一起转动而未发生滑动,B所受的静摩擦力最小 | |
| C. | 当转台转速增加时,A最先发生滑动 | |
| D. | 当转台转速继续增加时,A比B先滑动 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com